题目内容
下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )A.
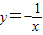
B.y=e|x|
C.y=-x2+3
D.y=cos
【答案】分析:根据题意,将x用-x代替判断解析式的情况利用偶函数的定义判断出为偶函数,然后根据反比例函数、对数函数、二次函数、三角数函数进行判定单调性即可得到结论.
解答:解:对于y=-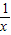 函数的定义域为{x|x≠0},f(-x)=-f(x),则该函数为奇函数,A不合题意
函数的定义域为{x|x≠0},f(-x)=-f(x),则该函数为奇函数,A不合题意
对于y=e|x|函数的定义域为x∈R,将x用-x代替函数的解析式不变,
所以y=e|x|是偶函数,但函数y=e|x|在(0,+∞)上单调单调递增,B符合题意
对于y=-x2+3函数的定义域为x∈R,将x用-x代替函数的解析式不变,
所以y=-x2+3是偶函数,但函数y=-x2+3在(0,+∞)上单调单调递减,C不合题意
对于y=cosx函数的定义域为x∈R,将x用-x代替函数的解析式不变,
所以y=cosx是偶函数,但函数y=cosx在(0,+∞)上不单调,D不合题意
故选B.
点评:本题主要考查了奇函数、偶函数的定义,以及常见函数的单调性的判定,属于基础题.
解答:解:对于y=-
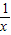 函数的定义域为{x|x≠0},f(-x)=-f(x),则该函数为奇函数,A不合题意
函数的定义域为{x|x≠0},f(-x)=-f(x),则该函数为奇函数,A不合题意对于y=e|x|函数的定义域为x∈R,将x用-x代替函数的解析式不变,
所以y=e|x|是偶函数,但函数y=e|x|在(0,+∞)上单调单调递增,B符合题意
对于y=-x2+3函数的定义域为x∈R,将x用-x代替函数的解析式不变,
所以y=-x2+3是偶函数,但函数y=-x2+3在(0,+∞)上单调单调递减,C不合题意
对于y=cosx函数的定义域为x∈R,将x用-x代替函数的解析式不变,
所以y=cosx是偶函数,但函数y=cosx在(0,+∞)上不单调,D不合题意
故选B.
点评:本题主要考查了奇函数、偶函数的定义,以及常见函数的单调性的判定,属于基础题.

练习册系列答案
相关题目
下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )
| A、y=x3 | B、y=cosx | C、y=ln|x| | D、y=2x |
下列函数中,既是偶函数又在区间(0,+∞)上是单调递减函数的是( )
A、f(x)=
| ||
| B、f(x)=-x2+1 | ||
C、f(x)=|
| ||
| D、f(x)=lg|x| |