题目内容
设数列{an}的前n项和为Sn,a1=1,nan=Sn+2n(n-1),n∈N*.
(1)求证:数列{an}为等差数列,并求{an}的通项公式an;
(2)是否存在正整数n使得 ?若存在,求出n值;若不存在,说明理由.
?若存在,求出n值;若不存在,说明理由.
解:(1)因为nan=Sn+2n(n-1),
当n≥2时(n-1)an-1=Sn-1+2(n-1)2-2(n-1),
两式作差,有(n-1)an-(n-1)an-1=4n-4,
?an-an-1=4,
又a1=1,所以an=4n-3;
(2)由(1)可知数列是等差数列,
所以Sn= =n(2n-1)?
=n(2n-1)? =2n-1,
=2n-1,
假设存在n满足题设条件,则(2-1)+(2×2-1)+(2×3-1)+…+(2n-1)-(n-1)2=2009,
1+3+5+…+(2n-1)-(n-1)2=2009,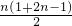 -(n-1)2=2009,
-(n-1)2=2009,
即2n-1=2009,所以n=1005.
分析:(1)通过nan=Sn+2n(n-1),写出当n≥2时(n-1)an-1=Sn-1+2(n-1)2-2(n-1),通过作差,证明数列{an}为等差数列,即可求出{an}的通项公式an;
(2)求出了的前n项和,求出 的表达式.然后利用等差数列求和,利用等式求出n的值即可.
的表达式.然后利用等差数列求和,利用等式求出n的值即可.
点评:本题考查数列的判断与证明,通项公式的求法,前n项和的求法,考查计算能力.
当n≥2时(n-1)an-1=Sn-1+2(n-1)2-2(n-1),
两式作差,有(n-1)an-(n-1)an-1=4n-4,
?an-an-1=4,
又a1=1,所以an=4n-3;
(2)由(1)可知数列是等差数列,
所以Sn=
 =n(2n-1)?
=n(2n-1)? =2n-1,
=2n-1,假设存在n满足题设条件,则(2-1)+(2×2-1)+(2×3-1)+…+(2n-1)-(n-1)2=2009,
1+3+5+…+(2n-1)-(n-1)2=2009,
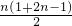 -(n-1)2=2009,
-(n-1)2=2009,即2n-1=2009,所以n=1005.
分析:(1)通过nan=Sn+2n(n-1),写出当n≥2时(n-1)an-1=Sn-1+2(n-1)2-2(n-1),通过作差,证明数列{an}为等差数列,即可求出{an}的通项公式an;
(2)求出了的前n项和,求出
 的表达式.然后利用等差数列求和,利用等式求出n的值即可.
的表达式.然后利用等差数列求和,利用等式求出n的值即可.点评:本题考查数列的判断与证明,通项公式的求法,前n项和的求法,考查计算能力.

练习册系列答案
相关题目