题目内容
设f(x)=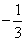 x3+
x3+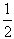 x2+2ax,
x2+2ax,
(1)若f(x)在(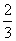 ,+∞)上存在单调递增区间,求a的取值范围;
,+∞)上存在单调递增区间,求a的取值范围;
(2)当0<a<2时,f(x)在[1,4]上的最小值为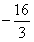 ,求f(x)在该区间上的最大值。
,求f(x)在该区间上的最大值。
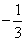 x3+
x3+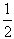 x2+2ax,
x2+2ax,(1)若f(x)在(
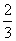 ,+∞)上存在单调递增区间,求a的取值范围;
,+∞)上存在单调递增区间,求a的取值范围;(2)当0<a<2时,f(x)在[1,4]上的最小值为
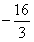 ,求f(x)在该区间上的最大值。
,求f(x)在该区间上的最大值。 解:(1)已知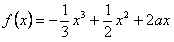 ,
,
∴ ,
,
函数f(x)在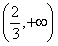 上存在单调递增区间,即导函数在
上存在单调递增区间,即导函数在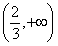 上存在函数值大于零的部分,
上存在函数值大于零的部分,
∴ ;
;
(2)已知0<a<2,f(x)在[1,4]上取到最小值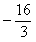 ,
,
而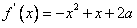 的图像开口向下,且对轴轴
的图像开口向下,且对轴轴 ,
,
∴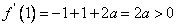 ,
,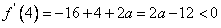 ,
,
则必有一点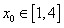 使得
使得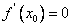 ,
,
此时函数f(x)在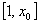 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
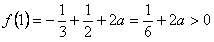 ,
,
∴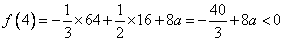 ,
,
∴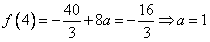 ,
,
此时,由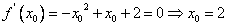 或-1(舍去),
或-1(舍去),
所以函数的最大值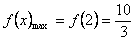 。
。
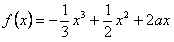 ,
,∴
 ,
,函数f(x)在
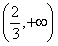 上存在单调递增区间,即导函数在
上存在单调递增区间,即导函数在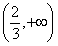 上存在函数值大于零的部分,
上存在函数值大于零的部分,∴
 ;
;(2)已知0<a<2,f(x)在[1,4]上取到最小值
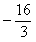 ,
,而
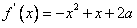 的图像开口向下,且对轴轴
的图像开口向下,且对轴轴 ,
, ∴
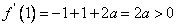 ,
,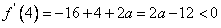 ,
,则必有一点
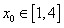 使得
使得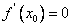 ,
,此时函数f(x)在
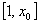 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,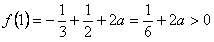 ,
,∴
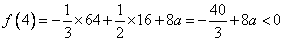 ,
,∴
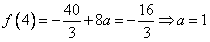 ,
,此时,由
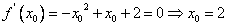 或-1(舍去),
或-1(舍去),所以函数的最大值
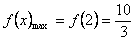 。
。
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目