题目内容
(12分)如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,DE =2AB=2,且F是CD的中点。
(Ⅰ)求证:AF//平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE;
(Ⅲ)设![]() ,当
,当![]() 为何值时?使得平面BCE与平面ACD所成的二面角的大小为
为何值时?使得平面BCE与平面ACD所成的二面角的大小为![]() 。
。

解:(I)取CE中点P,连结FP、BP,
∵F为CD的中点,∴FP//DE,且FP=![]() ………1分
………1分
又AB//DE,且AB=![]() ∴AB//FP,且AB=FP,
∴AB//FP,且AB=FP,
∴ABPF为平行四边形,∴AF//BP。…………………2分
 又∵AF
又∵AF![]() 平面BCE,BP
平面BCE,BP![]() 平面BCE,∴AF//平面BCE ……………………………………………………3分
平面BCE,∴AF//平面BCE ……………………………………………………3分
(II)∵△ACD为正三角形,∴AF⊥CD。
∵AB⊥平面ACD,DE//AB,
∴DE⊥平面ACD,又AF![]() 平面ACD,…………4分
平面ACD,…………4分
∴DE⊥AF。又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE。 …………5分
又BP//AF,∴BP⊥平面CDE。又∵BP![]() 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE。 …………………7分
(III)由(II),以F为坐标原点,FA,FD,FP所在的直线分别
为x,y,z轴(如图),建立空间直角坐标系F—xyz.
已知AC=2![]() ,则C(0,
,则C(0,![]() ,0),
,0),![]() ……8分
……8分
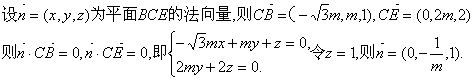 …9分
…9分
显然,![]() 为平面ACD的法向量。………………………………10分
为平面ACD的法向量。………………………………10分
设平面BCE与平面ACD所成的二面角为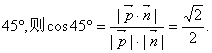
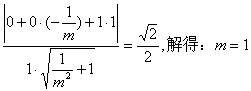
所以,当![]() 时,平面BCE与平面ACD所成的二面角为45°…………12分
时,平面BCE与平面ACD所成的二面角为45°…………12分

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.