题目内容
已知向量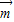 =(sinA,cosA),
=(sinA,cosA),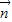 =(
=(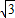 ,-1),(
,-1),(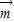 -
-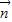 )⊥
)⊥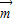 ,且A为锐角.
,且A为锐角.(Ⅰ) 求角A的大小;
(Ⅱ) 求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
【答案】分析:(Ⅰ)由题意得,利用两个向量的数量积的定义以及两个向量垂直的性质可得可得(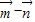 )•
)•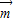 =0,解得
=0,解得
sin(A-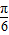 ) 的值,再由A为锐角求得A的值.
) 的值,再由A为锐角求得A的值.
(Ⅱ)由(Ⅰ)知cosA= ,化简f(x)=
,化简f(x)= -2
-2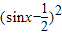 ,由sinx∈[-1,1],利用二次函数的性质求得
,由sinx∈[-1,1],利用二次函数的性质求得
f(x)的最大值和最小值,即可求得所求函数f(x)的值域.
解答:解:(Ⅰ)由题意得,向量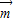 =(sinA,cosA),
=(sinA,cosA),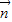 =(
=(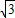 ,-1),可得
,-1),可得 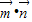 =
=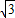 sinA-cosA,
sinA-cosA,
再由(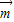 -
-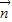 )⊥
)⊥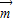 ,可得(
,可得(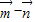 )•
)•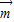 =
=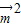 -
-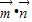 =1-
=1-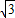 sinA+cosA=2sin(A-
sinA+cosA=2sin(A-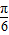 )-1=0,
)-1=0,
解得 sin(A-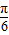 )=
)= .
.
再由A为锐角得 A-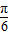 =
=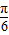 ,故有A=
,故有A=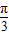 .
.
(Ⅱ)由(Ⅰ)知cosA= ,所以f(x)=cos2x+2sinx=1-2sin2x+2sinx=
,所以f(x)=cos2x+2sinx=1-2sin2x+2sinx= -2
-2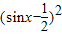 ,
,
因为x∈R,所以sinx∈[-1,1],因此,当sinx= 时,f(x)有最大值
时,f(x)有最大值 ,
,
当sinx=-1时,f(x)有最小值-3,所以所求函数f(x)的值域是[-3, ].
].
点评:本题主要考查两个向量坐标形式的运算,两个向量垂直的性质,三角函数的恒等变换及化简求值,复合三角
函数的单调性,二次函数的性质应用,属于中档题.
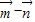 )•
)•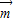 =0,解得
=0,解得 sin(A-
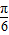 ) 的值,再由A为锐角求得A的值.
) 的值,再由A为锐角求得A的值.(Ⅱ)由(Ⅰ)知cosA=
 ,化简f(x)=
,化简f(x)= -2
-2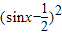 ,由sinx∈[-1,1],利用二次函数的性质求得
,由sinx∈[-1,1],利用二次函数的性质求得f(x)的最大值和最小值,即可求得所求函数f(x)的值域.
解答:解:(Ⅰ)由题意得,向量
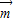 =(sinA,cosA),
=(sinA,cosA),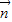 =(
=(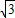 ,-1),可得
,-1),可得 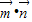 =
=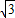 sinA-cosA,
sinA-cosA,再由(
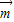 -
-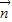 )⊥
)⊥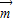 ,可得(
,可得(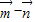 )•
)•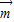 =
=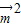 -
-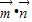 =1-
=1-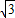 sinA+cosA=2sin(A-
sinA+cosA=2sin(A-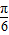 )-1=0,
)-1=0,解得 sin(A-
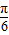 )=
)= .
.再由A为锐角得 A-
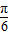 =
=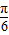 ,故有A=
,故有A=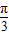 .
.(Ⅱ)由(Ⅰ)知cosA=
 ,所以f(x)=cos2x+2sinx=1-2sin2x+2sinx=
,所以f(x)=cos2x+2sinx=1-2sin2x+2sinx= -2
-2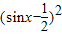 ,
,因为x∈R,所以sinx∈[-1,1],因此,当sinx=
 时,f(x)有最大值
时,f(x)有最大值 ,
,当sinx=-1时,f(x)有最小值-3,所以所求函数f(x)的值域是[-3,
 ].
].点评:本题主要考查两个向量坐标形式的运算,两个向量垂直的性质,三角函数的恒等变换及化简求值,复合三角
函数的单调性,二次函数的性质应用,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目