题目内容
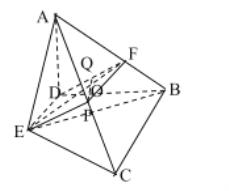
【题目】图①中△ABC 为直角三角形![]() D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
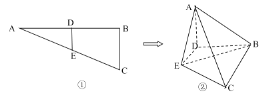
(1)在线段AC上找一点P,使EP∥平面ABD,并求出异面直线AB、EP所成的角;
(2)在平面ABD内找一点Q,使PQ⊥平面ABE,并求三棱锥P-ABE的体积.
【答案】(1)点P为AC的中点,![]() (2)Q为DF的中点,
(2)Q为DF的中点,![]()
【解析】
(1)分别取 AC、AB 的中点 P、F,依次连 EP、PF、FD,先证四边形![]() 为平行四边形,再利用线面平行的判定即可得解;由等腰三角形的性质可得
为平行四边形,再利用线面平行的判定即可得解;由等腰三角形的性质可得![]() ,即可得
,即可得![]() ,即可得解;
,即可得解;
(2)过P作![]() 并延长DF于Q,先证明
并延长DF于Q,先证明![]() 平面ABE,再通过平面几何知识求证
平面ABE,再通过平面几何知识求证![]() 即可得解;求出
即可得解;求出![]() 和PO长度即可求得体积.
和PO长度即可求得体积.
(1)分别取 AC、AB 的中点 P、F,依次连 EP、PF、FD,
则![]() 且
且![]() ,
,
![]() D、E 分别为 AB、AC 的中点,
D、E 分别为 AB、AC 的中点,
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() 即四边形
即四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
即所求的点P为AC的中点,
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
故异面直线 AB、EP 所成的夹角为![]()
(2)连结EF,因为![]() ,
,![]() ,
,![]()
![]() 平面ABD,
平面ABD,
![]() 平面ABD,
平面ABD,![]()
![]() ,
,
又![]() ,
,![]() ,
,![]()
![]() 平面DEPF,
平面DEPF,
又![]() 平面ABE,
平面ABE,
![]() 平面
平面![]() 平面DEPF,且平面
平面DEPF,且平面![]() 平面
平面![]() ,
,
在平面DEPF中,过P作![]() 并延长DF于Q,则
并延长DF于Q,则![]() 平面ABE,
平面ABE,
因为四边形DEPF是矩形,且PF=DE=1,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
知Q为DF的中点,
在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
所以![]() .
.

练习册系列答案
相关题目