题目内容
第29届奥运会在北京举行.设数列an=logn+1(n+2)(n∈N*).定义使a1•a2•a3•…•ak为整数的实数k为奥运吉祥数,则在区间[1,2 008]内的所有奥运吉祥数之和为
- A.1004
- B.2026
- C.4072
- D.2044
B
分析:先利用对数的运算性质求出实数k,再对所有实数k值进行分组求和.
解答:an=logn+1(n+2)=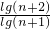 ,
,
a1•a2•a3••ak= .
.
由题意知k+2=22,23,,210,
∴k=22-2,23-2,,210-2.
∴S=(22+23++210)-2×9= .
.
故选 B
点评:本题是对对数运算性质及分组求数列和的综合考查,是基础题.
分析:先利用对数的运算性质求出实数k,再对所有实数k值进行分组求和.
解答:an=logn+1(n+2)=
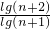 ,
,a1•a2•a3••ak=
 .
.由题意知k+2=22,23,,210,
∴k=22-2,23-2,,210-2.
∴S=(22+23++210)-2×9=
 .
.故选 B
点评:本题是对对数运算性质及分组求数列和的综合考查,是基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
第29届奥运会在北京举行.设数列an=logn+1(n+2)(n∈N*).定义使a1•a2•a3•…•ak为整数的实数k为奥运吉祥数,则在区间[1,2 008]内的所有奥运吉祥数之和为( )
| A、1004 | B、2026 | C、4072 | D、2044 |