题目内容
已知二次函数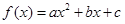 的导数为
的导数为 ,
,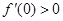 ,对于任意实数
,对于任意实数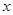 ,有
,有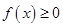 ,则
,则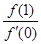 的最小值为( )
的最小值为( )
A.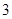 | B.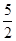 | C.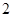 | D.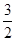 |
C
解析试题分析:因为 ,所以
,所以 。因为对于任意实数
。因为对于任意实数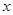 ,有
,有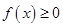 ,所以
,所以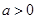 且
且 。综上可得
。综上可得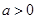 ,
, ,
,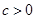 且
且 ,所以
,所以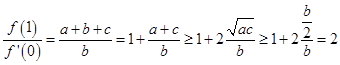 。当且仅当
。当且仅当 时取
时取 。故C正确。
。故C正确。
考点:1求导;2恒成立问题;3基本不等式。

练习册系列答案
相关题目
函数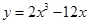 在区间
在区间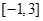 上的最大值和最小值分别为
上的最大值和最小值分别为
A.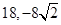 | B.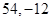 | C.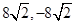 | D.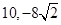 |
若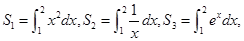 则
则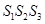 的大小关系为( )
的大小关系为( )
A.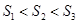 | B.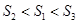 |
C. | D.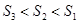 |
函数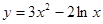 的单调增区间为( )
的单调增区间为( )
A.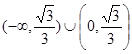 | B.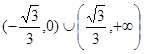 |
C.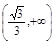 | D.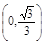 |
设函数
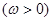 的导数
的导数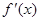 的最大值为3,则
的最大值为3,则 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是
A.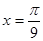 | B. | C.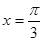 | D.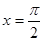 |
若函数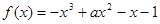 在
在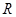 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( )
A.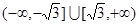 | B.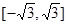 |
C.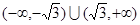 | D.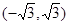 |
某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第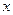 小时,原油温度(单位:℃)为
小时,原油温度(单位:℃)为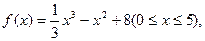 ,那么原油温度的瞬时变化率的最小值为( )
,那么原油温度的瞬时变化率的最小值为( )
| A.8 |
B.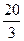 |
| C.-1 |
| D.-8 |
直线y=a与函数y=x3-3x的图象有三个相异的交点,则a的取值范围为 ( ).
| A.(-2,2) | B.[-2,2] |
| C.[2,+∞) | D.(-∞,-2] |
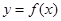 的导函数在区间
的导函数在区间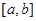 上是增函数,则函数
上是增函数,则函数