题目内容
数列{an}的前n项和记为Sn,已知an=5Sn-3(n∈N)求 (a1+a3+…+a2n-1)的值.
(a1+a3+…+a2n-1)的值.
解:由Sn=a1+a2++an知
an=Sn-Sn-1(n≥2),
a1=S1,
由已知an=5Sn-3得
an-1=5Sn-1-3.
于是an-an-1
=5(Sn-Sn-1)
=5an,
所以an=- an-1.
an-1.
由a1=5S1-3,
得a1= .
.
所以,数列{an}是首项a1= ,公比q=-
,公比q=- 的等比数列.
的等比数列.
由此知数列a1,a3,a5,,a2n-1,
是首项为a1= ,公比为
,公比为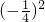 的等比数列.
的等比数列.
∴ (a1+a3+a5++a2n-1)=
(a1+a3+a5++a2n-1)= .
.
分析:由题意可知数列{an}是首项a1= ,公比q=-
,公比q=- 的等比数列.由此知数列a1,a3,a5,,a2n-1是首项为a1=
的等比数列.由此知数列a1,a3,a5,,a2n-1是首项为a1= ,公比为
,公比为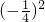 的等比数列.由此可以求出
的等比数列.由此可以求出 (a1+a3+a5++a2n-1)的值.
(a1+a3+a5++a2n-1)的值.
点评:本题主要考查等比数列和数列极限等基础知识,解题时要注意培养计算能力.
an=Sn-Sn-1(n≥2),
a1=S1,
由已知an=5Sn-3得
an-1=5Sn-1-3.
于是an-an-1
=5(Sn-Sn-1)
=5an,
所以an=-
 an-1.
an-1.由a1=5S1-3,
得a1=
 .
.所以,数列{an}是首项a1=
 ,公比q=-
,公比q=- 的等比数列.
的等比数列.由此知数列a1,a3,a5,,a2n-1,
是首项为a1=
 ,公比为
,公比为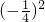 的等比数列.
的等比数列.∴
 (a1+a3+a5++a2n-1)=
(a1+a3+a5++a2n-1)= .
.分析:由题意可知数列{an}是首项a1=
 ,公比q=-
,公比q=- 的等比数列.由此知数列a1,a3,a5,,a2n-1是首项为a1=
的等比数列.由此知数列a1,a3,a5,,a2n-1是首项为a1= ,公比为
,公比为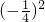 的等比数列.由此可以求出
的等比数列.由此可以求出 (a1+a3+a5++a2n-1)的值.
(a1+a3+a5++a2n-1)的值.点评:本题主要考查等比数列和数列极限等基础知识,解题时要注意培养计算能力.

练习册系列答案
相关题目