题目内容
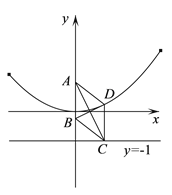
【题目】已知菱形![]() ,
,![]() 在
在![]() 轴上且
轴上且![]() ,
,![]()
![]() (
(![]() ,
,![]() ).
).
(Ⅰ)求![]() 点轨迹
点轨迹![]() 的方程;
的方程;
(Ⅱ)延长![]() 交轨迹
交轨迹![]() 于点
于点![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为圆心,线段
为圆心,线段![]() 为半径的圆与直线
为半径的圆与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
【答案】(Ⅰ)![]() (
(![]() );(Ⅱ)答案见解析.
);(Ⅱ)答案见解析.
【解析】试题分析:
(Ⅰ)由题意可知对角线![]() 与
与![]() 垂直平分,由题意结合垂直平分线的性质可得点
垂直平分,由题意结合垂直平分线的性质可得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 到
到![]() 点的距离相等,结合几何关系可知
点的距离相等,结合几何关系可知![]() 点轨迹方程为
点轨迹方程为![]() (
(![]() ).
).
(Ⅱ)设![]() ,
,![]() ,联立直线AD是方程与抛物线方程可得
,联立直线AD是方程与抛物线方程可得![]() ,由题意结合韦达定理可得
,由题意结合韦达定理可得![]() ,
,![]() ,
,![]() ,利用导数研究切线方程可得在点
,利用导数研究切线方程可得在点![]() 处的切线方程为:
处的切线方程为:![]() ,且直线
,且直线![]() 的方程为
的方程为![]() ,据此可得交点坐标
,据此可得交点坐标![]() ,即
,即![]() ,计算可得点
,计算可得点![]() 到直线
到直线![]() 的距离
的距离![]() ,则圆与直线相切.
,则圆与直线相切.
试题解析:
(Ⅰ)因为![]() 是菱形,所以对角线
是菱形,所以对角线![]() 与
与![]() 垂直平分,
垂直平分,
因为![]() 在
在![]() 轴上,所以
轴上,所以![]() 与直线
与直线![]() 垂直,
垂直,
所以点![]() 到直线
到直线![]() 的距离与
的距离与![]() 到
到![]() 点的距离相等,
点的距离相等,
所以![]() 点轨迹
点轨迹![]() 为抛物线(不包含顶点),
为抛物线(不包含顶点),
其轨迹方程为![]() (
(![]() ).
).
(Ⅱ)设![]() ,
,![]() ,
,
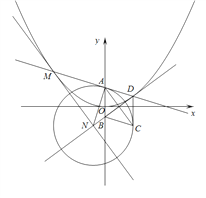
设直线![]() 的方程为
的方程为![]() ,联立
,联立![]() 可得:
可得:![]()
所以![]() ,
,![]() .
.
因为菱形![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]()
由![]() 可得
可得![]()
所以在点![]() 处的切线方程的斜率为
处的切线方程的斜率为![]()
则切线的方程为:![]() ,即
,即![]() ……①
……①
因为![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() 中点
中点![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]()
![]() ②
②
联立①②可得 ,即点
,即点![]() ,又
,又![]() ,所以
,所以![]()
所以![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]()
所以圆与直线相切.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
