题目内容
把函数 的图象向左平移
的图象向左平移 后,所得函数的解析式是
后,所得函数的解析式是
A. | B. | C. | D. |
C
解析试题分析:对于图像的平移变换的求解解析式,首先要明白,变换影响的是x的值。
那么可知函数 的图象向左平移
的图象向左平移 后,得到的解析式为
后,得到的解析式为 ,故选C.
,故选C.
考点:本试题主要是考查了三角函数图像的变换。
点评:利用平移变换解题的时候,关键是理解,平移变换是针对每一个点的横坐标而言的,因此是对x加上 ,然后求解得到解析式,属于基础题。
,然后求解得到解析式,属于基础题。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
设 是正实数,函数
是正实数,函数 在
在 上是增函数,那么
上是增函数,那么 的最大值是
的最大值是
A. | B.2 | C. | D.3 |
已知 等于( )
等于( )
A. | B. | C.—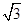 | D.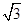 |
为得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
若函数 在
在 上有零点,则
上有零点,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知 ,则tanx等于( )
,则tanx等于( )
A. | B. | C. | D. |
设 ,函数
,函数 的图像向右平移
的图像向右平移 个单位
个单位
后与原图像重合,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
| D.3 |
 的图像与x轴的交点的横坐标构成一个公差为
的图像与x轴的交点的横坐标构成一个公差为 的等差数列,要得到函数
的等差数列,要得到函数 的图像,只需将
的图像,只需将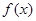 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向右平移
个单位 D.向右平移