Question

若双曲线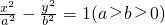的左、右焦点分别为F₁，F₂，线段F₁F₂被抛物线y²=2bx的焦点分成5：3两段，则此双曲线的离心率为________．

Answer 1

分析：依题意，可求得抛物线y²=2bx的焦点F（，0），由=即可求得b，c之间的关系，从而可求得此双曲线的离心率．
解答：∵抛物线y²=2bx的焦点F（，0），双曲线-=1（a＞b＞0）左、右焦点F₁（-c，0），F₂（c，0），
又线段F₁F₂被抛物线y²=2bx的焦点分成5：3两段，
∴=，即=，
∴c=2b；
又c²=a²+b²=4b²，
∴a²=3b²，
∴此双曲线的离心率e²===，
∴e==．
故答案为：．
点评：本题考查双曲线的简单性质，由=即可求得b，c之间的关系是关键，考查分析与运算能力，属于中档题．