题目内容
函数f（x）=
是奇函数，则a+b=________．
1
分析：直接利用奇函数定义域内0则f（0）=0求出a，再根据其为奇函数得f（1）=-f（-1）求出b即可求出结论．
解答：有函数解析式可得：其为定义在实数集R上的奇函数．
所以有：f（0）=0，∴a=0，
又∵f（1）=-f（-1）
∴0=-[（-1）+b]?b=1．
∴a+b=1．
故答案为：1．
点评：本题主要考查奇函数的性质．当一个函数是定义在实数集R上的奇函数时，一定有f（0）=0．
分析：直接利用奇函数定义域内0则f（0）=0求出a，再根据其为奇函数得f（1）=-f（-1）求出b即可求出结论．
解答：有函数解析式可得：其为定义在实数集R上的奇函数．
所以有：f（0）=0，∴a=0，
又∵f（1）=-f（-1）
∴0=-[（-1）+b]?b=1．
∴a+b=1．
故答案为：1．
点评：本题主要考查奇函数的性质．当一个函数是定义在实数集R上的奇函数时，一定有f（0）=0．
练习册系列答案
名校课堂系列答案
相关题目
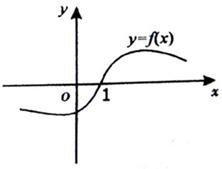已知函数f（x）（x∈R）的一段图象如图所示，f′（x）是函f（x）（数的导函数，且y=f（x+1）是奇函数，给出以下结论：
已知函数f（x）（x∈R）的一段图象如图所示，f′（x）是函f（x）（数的导函数，且y=f（x+1）是奇函数，给出以下结论：