题目内容
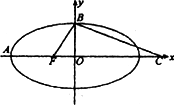
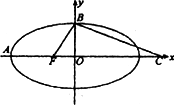
点P是椭圆
＝1上的一点，F1、F2是焦点，且∠F1PF2＝30°，求△F1PF2的面积．
答案：
解析：
解析：
|
解析：在椭圆 ∵点P在椭圆上， ∴|PF1|＋|PF2|＝2a＝ 由余弦定理知|PF1|2＋|PF2|2－2|PF1||PF2|·cos30°＝|F1F2|2＝4 ② ①－②得(2＋ ∴|PF1||PF2|＝16(2－ ∴ |
＝1中，a＝
，b＝2，∴c＝
＝1．
，|PF1|2＋|PF2|2＋2|PF1||PF2|＝20 ①
)|PF1||PF2|＝16，
＝
|PF1||PF2|·sin30°＝8－
．
练习册系列答案
相关题目
＝1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为
，点C在x轴上，BC⊥BD，B，C，F三点确定的圆M恰好与直线x＋
y＋3＝0相切．
＝1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为
，点C在x轴上，BC⊥BF，B，C，F三点确定的圆M恰好与直线x＋
y＋3＝0相切．
，离心率
，M是椭圆上的动点．
，求|MC|·|MD|的最大值；
，
．求线段QB的中点P的轨迹方程；
＝1(a＞b＞0)上的一个动点，F1，F2分别为椭圆的左、右焦点，弦AB过点F2，当AB⊥x轴时，恰好有|AF1|＝3|AF2|．
：
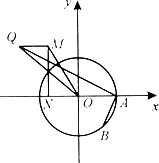
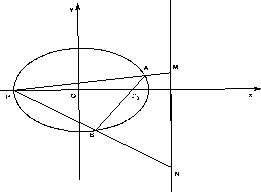
＝1的右焦点，点P是椭圆
：
＋
＝
上的动点．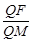
＝e (e为椭圆的离心率)？若存在，求出点M的坐标；若不存在，请说明理由．