题目内容
△PF1F2的一个顶点P(7,12)在双曲线x2-
=1上,另外两顶点F1、F2为该双曲线的左、右焦点,则△PF1F2的内心的横坐标为
| y2 | b2 |
1
1
.分析:通过已知条件求出b,充分利用平面几何图形的性质解题.因从同一点出发的切线长相等,得PM|=|PN|,|F1M|=|F1D|,|F2N|=|F2D|,再结合双曲线的定义得|F1D|-|F2D|=2a,从而即可求得△PF1F2的内心的横坐标.
解答: 解:P(7,12)在双曲线x2-
解:P(7,12)在双曲线x2-
=1上,
所以72-
=1,b2=3,
双曲线方法为:x2-
=1.
记△PF1F2的内切圆圆心为C,边PF1、PF2、F1F2上的切点分别为M、N、D,易见C、D横坐标相等,
|PM|=|PN|,|F1M|=|F1D|,|F2N|=|F2D|,由|PF1|-|PF2|=2,
即:|PM|+|MF1|-(|PN|+|NF2|)=2,得|MF1|-|NF2|=2即|F1D|-|F2D|=2,
记C的横坐标为x0,则D(x0,0),
于是:x0+c-(c-x0)=2,
得x0=1,
故答案为:1.
 解:P(7,12)在双曲线x2-
解:P(7,12)在双曲线x2-| y2 |
| b2 |
所以72-
| 122 |
| b2 |
双曲线方法为:x2-
| y2 |
| 3 |
记△PF1F2的内切圆圆心为C,边PF1、PF2、F1F2上的切点分别为M、N、D,易见C、D横坐标相等,
|PM|=|PN|,|F1M|=|F1D|,|F2N|=|F2D|,由|PF1|-|PF2|=2,
即:|PM|+|MF1|-(|PN|+|NF2|)=2,得|MF1|-|NF2|=2即|F1D|-|F2D|=2,
记C的横坐标为x0,则D(x0,0),
于是:x0+c-(c-x0)=2,
得x0=1,
故答案为:1.
点评:本题主要考查了双曲线的定义、双曲线的应用及转化问题的能力,属于基础题.

练习册系列答案
相关题目
 (2012•茂名二模)如图所示,圆柱底面的直径AB长度为2
(2012•茂名二模)如图所示,圆柱底面的直径AB长度为2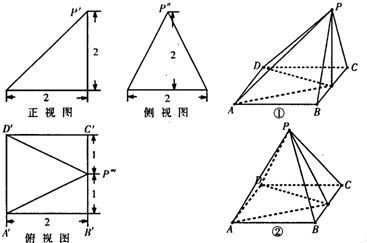 已知某几何体的三视图如图所示,其中P',P'',P''分别是该几何体的一个顶点P在三个投影面上的投影,A',B',C',D'分别是另四个顶点A,B,C,D的投影.
已知某几何体的三视图如图所示,其中P',P'',P''分别是该几何体的一个顶点P在三个投影面上的投影,A',B',C',D'分别是另四个顶点A,B,C,D的投影. 上,另外两顶点F1、F2为该双曲线的左、右焦点,则△PF1F2的内心的横坐标为________.
上,另外两顶点F1、F2为该双曲线的左、右焦点,则△PF1F2的内心的横坐标为________. 上,另外两顶点F1、F2为该双曲线的左、右焦点,则△PF1F2的内心的横坐标为 .
上,另外两顶点F1、F2为该双曲线的左、右焦点,则△PF1F2的内心的横坐标为 .