题目内容
已知数列{an}满足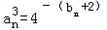 (n∈N*),数列{bn}前n项和
(n∈N*),数列{bn}前n项和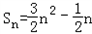 ,数列{cn}满足cn=anbn.
,数列{cn}满足cn=anbn.
(1)求数列{an}和数列{bn}的通项公式;
(2)求数列{cn}的前n项和Tn;
(3)若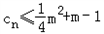 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
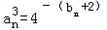 (n∈N*),数列{bn}前n项和
(n∈N*),数列{bn}前n项和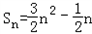 ,数列{cn}满足cn=anbn.
,数列{cn}满足cn=anbn.(1)求数列{an}和数列{bn}的通项公式;
(2)求数列{cn}的前n项和Tn;
(3)若
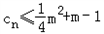 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.解:(1)由已知得,当n≥2时,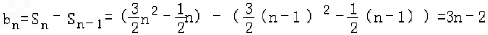 ,
,
又b1=1=3×1﹣2,符合上式.
故数列{bn}的通项公式bn=3n﹣2.
又∵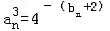 ,
,
∴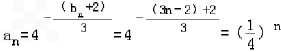 ,
,
故数列{an}的通项公式为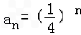 .
.
(2)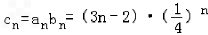 ,
,
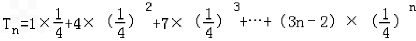 ①,
①,
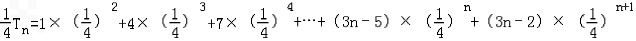 ②,
②,
①﹣②得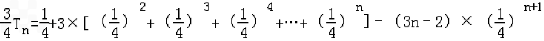
=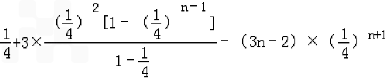 =
=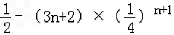 ,
,
∴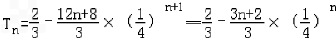 .
.
(3)∵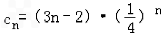 ,
,
∴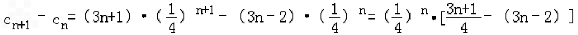
=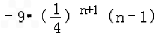 ,
,
当n=1时,cn+1=cn;
当n≥2时,cn+1≤cn,
∴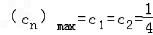 .
.
若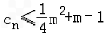 对一切正整数n恒成立,则只要
对一切正整数n恒成立,则只要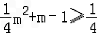 即可,
即可,
(m+5)(m﹣1)≥0,解得 m≤﹣5,或m≥1,
故实数m的取值范围为(﹣∞,﹣5]∪[1,+∞).
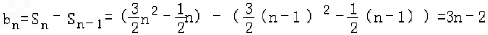 ,
,又b1=1=3×1﹣2,符合上式.
故数列{bn}的通项公式bn=3n﹣2.
又∵
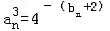 ,
,∴
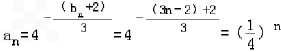 ,
,故数列{an}的通项公式为
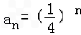 .
.(2)
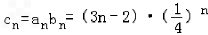 ,
,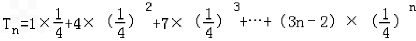 ①,
①,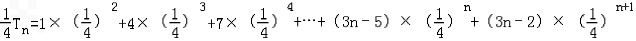 ②,
②,①﹣②得
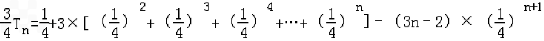
=
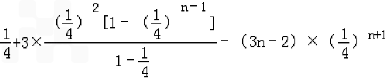 =
=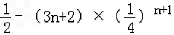 ,
,∴
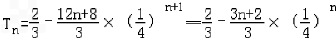 .
.(3)∵
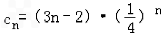 ,
,∴
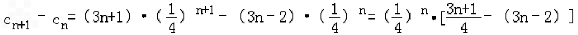
=
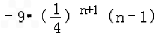 ,
,当n=1时,cn+1=cn;
当n≥2时,cn+1≤cn,
∴
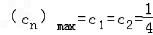 .
.若
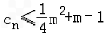 对一切正整数n恒成立,则只要
对一切正整数n恒成立,则只要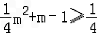 即可,
即可,(m+5)(m﹣1)≥0,解得 m≤﹣5,或m≥1,
故实数m的取值范围为(﹣∞,﹣5]∪[1,+∞).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目