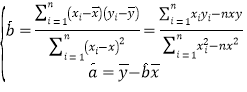题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 为短轴的一个端点且
为短轴的一个端点且![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)求椭圆的方程;
(2)若![]() 、
、![]() 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点![]() 满足
满足![]() ,连接
,连接![]() ,交椭圆于点
,交椭圆于点![]() ,试问
,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 、
、![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)存在定点
;(2)存在定点![]() ,理由见解析
,理由见解析
【解析】
(1)本题首先可以根据![]() 得出
得出![]() 、
、![]() 的值,然后通过
的值,然后通过![]() 、
、![]() 的值即可计算得出
的值即可计算得出![]() 的值并得出椭圆方程;
的值并得出椭圆方程;
(2)本题首先可以根据(1)中结论得出![]() 、
、![]() 两点坐标,然后设出直线
两点坐标,然后设出直线![]() 的方程以及
的方程以及![]() 点坐标,再然后联立椭圆以及直线
点坐标,再然后联立椭圆以及直线![]() 方程得出
方程得出![]() 以及
以及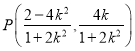 ,最后根据
,最后根据![]() 即可得出结果。
即可得出结果。
(1)因为![]() ,
,
所以![]() ,
,![]() ,
,
所以椭圆方程为![]() 。
。
(2)由(1)可知![]() ,
,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,则
,则![]() ,
,
联立椭圆以及直线![]() 可得
可得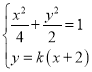 ,整理得
,整理得![]() ,
,
方程显然有两个解,由韦达定理可得![]() ,得
,得![]() ,
,![]() ,
,
所以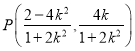 ,
,
设![]() ,若存在满足题设的
,若存在满足题设的![]() 点,则
点,则![]() ,
,
由![]() ,整理可得
,整理可得![]() 恒成立,
恒成立,
所以![]() ,故存在定点
,故存在定点![]() 满足题设要求。
满足题设要求。

【题目】对某校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
问:(1)由题意列出学生语文成绩与外语成绩关系的![]() 列联表:
列联表:
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | |||
外语不优秀 | |||
总计 |
(2)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?(保留三位小数)
(附: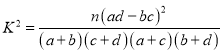 )
)
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
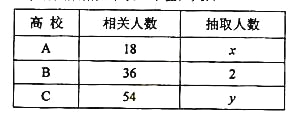
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
(I)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(II)求![]() 关于
关于![]() 的线性回归方程;若该设备的价格是每台
的线性回归方程;若该设备的价格是每台![]() 万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: