题目内容
下列命题中,真命题是( )
| A.?m∈R,使函数f(x)=x2+mx(x∈R)是偶函数 |
| B.?m∈R,使函数f(x)=x2+mx(x∈R)是奇函数 |
| C.?m∈R,使函数f(x)=x2+mx(x∈R)都是偶函数 |
| D.?m∈R,使函数f(x)=x2+mx(x∈R)都是奇函数 |
A、当m=0时,函数f(x)=x2是偶函数,故A正确;
B、f(-x)=x2-mx,-f(x)=-x2-mx,不存在m使函数在定义域内对任意的x都有f(-x)=-f(x),故B错误;
C、仅当m=0时f(x)是偶函数,m取其它值均不满足题意,故C错误;
D、一个m也没有更谈不上对任意的m的值,故D错误.
故选A.
B、f(-x)=x2-mx,-f(x)=-x2-mx,不存在m使函数在定义域内对任意的x都有f(-x)=-f(x),故B错误;
C、仅当m=0时f(x)是偶函数,m取其它值均不满足题意,故C错误;
D、一个m也没有更谈不上对任意的m的值,故D错误.
故选A.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
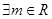 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1