Question

如图，直三棱柱ABC-A₁B₁C₁中，AB⊥BC，E是A₁C的中点，ED⊥A₁C且交AC于D,A₁A=AB=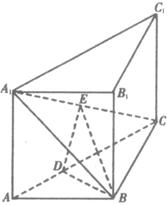BC．

(Ⅰ)证明：A₁C⊥平面EBD；

(Ⅱ)求平面A₁AB与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)．

Answer 1

(1)证明：∵三棱柱ABC-A₁B₁C₁中A₁A⊥AB，∴Rt△A₁AB中AB=

∴BC=A₁B∴△A₁BC是等腰三角形

∵E是等腰△A₁BC底边A₁C上的中点,

∴A₁C⊥BE            ①

又依条件知A₁C⊥ED,   ②

且ED∩BE=E，        ③

由①,②，③得A₁C⊥平面EBD 

(2)∵A₁A、ED平面A₁AC，且A₁A、ED不平行.

故延长A₁A、ED后必相交，设交点为F，连接FB

∴A₁-FB-E是所求的二面角.

依条件易证明Rt△A₁EF≌Rt△A₁AC.

∵E为A₁C中点，∴A为A₁F中点

∴AF=A₁A=AB，∴∠A₁BA=∠ABF=45 .

∴∠A₁BF=90 .即A₁B⊥FB.

又A₁E⊥平面EFB,

∴EF⊥FB

∴∠A₁BE是所求的二面角的平面角.

E是等腰三角形A₁BC底边中点,

∵∠A₁BE=45 .故所求的二面角的大小为45 .