题目内容
设函数f(x)=kax-a-x(a>0且a≠1)是奇函数,(1)求k的值;
(2)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(3)若
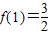 ,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求m的值.
,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求m的值.
【答案】分析:(1)根据奇函数的性质知道f(0)=0,即可得答案.
(2)由(1)可得f(x)的解析式,再根据f(x)的单调性求出不等式的解集.
(3)由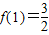 课求出a的值,进而求出函数g(x)的解析式.再根据g(x)在[1,+∞)上的最小值为-2,求出m的值
课求出a的值,进而求出函数g(x)的解析式.再根据g(x)在[1,+∞)上的最小值为-2,求出m的值
解答:解:(1)∵f(x)为奇函数,
∴f(0)=0,∴k-1=0,
∴k=1
(2)∵f(1)>0,∴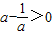 ,∴a>1,
,∴a>1,
又f'(x)=axlna+a-xlna=(ax+a-x)lna>0
∴f(x)在R上单调递增,
原不等式可化为:f(x2+2x)>f(4-x),
∴x2+2x>4-x,即x2+3x-4>0,
∴x>1或x<-4,
∴不等式的解集为{x|x>1或x<-4}
(3)∵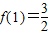 ,∴
,∴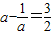 ,即2a2-3a-2=0,
,即2a2-3a-2=0,
∴a=2或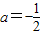 (舍去)
(舍去)
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2
令t=f(x)=2x-2-x,
∵x≥1,∴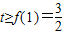 ,
,
∴g(x)=t2-2mt+2=(t-m)2+2-m2,
当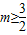 时,当t=m时,g(x)min=2-m2=-2,
时,当t=m时,g(x)min=2-m2=-2,
∴m=2,
当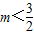 时,当
时,当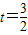 时,
时,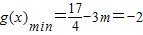 ,
,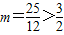 ,舍去,
,舍去,
∴m=2.
点评:本题主要考查函数奇偶性的问题,这里要求会根据单调性进行解不等式.
(2)由(1)可得f(x)的解析式,再根据f(x)的单调性求出不等式的解集.
(3)由
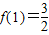 课求出a的值,进而求出函数g(x)的解析式.再根据g(x)在[1,+∞)上的最小值为-2,求出m的值
课求出a的值,进而求出函数g(x)的解析式.再根据g(x)在[1,+∞)上的最小值为-2,求出m的值解答:解:(1)∵f(x)为奇函数,
∴f(0)=0,∴k-1=0,
∴k=1
(2)∵f(1)>0,∴
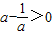 ,∴a>1,
,∴a>1,又f'(x)=axlna+a-xlna=(ax+a-x)lna>0
∴f(x)在R上单调递增,
原不等式可化为:f(x2+2x)>f(4-x),
∴x2+2x>4-x,即x2+3x-4>0,
∴x>1或x<-4,
∴不等式的解集为{x|x>1或x<-4}
(3)∵
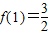 ,∴
,∴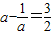 ,即2a2-3a-2=0,
,即2a2-3a-2=0,∴a=2或
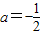 (舍去)
(舍去)∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2
令t=f(x)=2x-2-x,
∵x≥1,∴
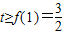 ,
,∴g(x)=t2-2mt+2=(t-m)2+2-m2,
当
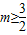 时,当t=m时,g(x)min=2-m2=-2,
时,当t=m时,g(x)min=2-m2=-2,∴m=2,
当
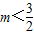 时,当
时,当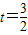 时,
时,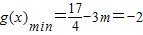 ,
,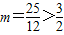 ,舍去,
,舍去,∴m=2.
点评:本题主要考查函数奇偶性的问题,这里要求会根据单调性进行解不等式.

练习册系列答案
相关题目
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k. 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.