题目内容

若函数f(x)=a-bsinx的最大值为,最小值为-,求函数y=1-acosbx的最值和周期.

解：（1）b＞0,当sinx=-1时，f(x)max=;

当sinx=1时，f(x)min=-.

于是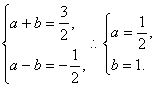

b=1.此时b=1＞0符合题意，∴y=1-cosx.

(2)b=0,此时f(x)=a,这与f(x)有最大值,最小值-矛盾.故b=0不成立.

（3）b＜0,由题意，得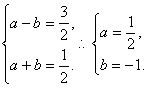符合题意.

∴y=1-cos(-x),即y=1-cosx.

综上可知，函数y=1-cosx，它的最大值为,最小值为-，周期为2π.

练习册系列答案
相关题目
给出下列四个命题：
①若函数f(x)=a(x3-x)在区间(-
3
3
，
3
3
)为减函数，则a＞0；
②函数f(x)=lg(ax+1)的定义域是{x|x＞-
1
a
}；
③当x＞0且x≠1时，有lnx+
1
lnx
≥2；
④若M是圆（x-5）2+（y+2）2=34上的任意一点，则点M关于直线y=ax-5a-2的对称点M′也在该圆上．
所有正确命题的序号是
 
若函数f(x)=
(a-2)xx≥2
(
1
2
)x-1		x＜2
是R上的单调减函数，则实数a的取值范围是（　　）
A、（-∞，2）
B、(-∞，
13
8
]
C、（0，2）
D、[
13
8
，2)
若函数f(x)=(a-
1
ex+1
)x是偶函数，则f（ln2）=
1
6
ln2
1
6
ln2
．
对于函数y=f（x），如果存在区间[m，n]，同时满足下列条件：①f（x）在[m，n]内是单调的；②当定义域是[m，n]时，f（x）的值域也是[m，n]，则称[m，n]是该函数的“和谐区间”．若函数f(x)=
a+1
a
-
1
x
(a＞0)有“和谐区间”，则函数g(x)=
1
3
x3+
1
2
ax2+(a-1)x+5的极值点x1，x2满足（　　）
A、x1∈（0，1），x2∈（1，+∞）
B、x1∈（-∞，0），x2∈（0，1）
C、x1∈（-∞，0），x2∈（-∞，0）
D、x1∈（1，+∞），x2∈（1，+∞）
若函数f(x)=
(a-2)x+3a-2，0≤x≤2
ax，x＞2
是一个单调递增函数，则实数a的取值范围（　　）
A、（1，2]∪[3，+∞）
B、（1，2]
C、（0，2]∪[3，+∞）
D、[3，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网