题目内容
在体积为V的三棱锥S-ABC的棱AB上任取一点P,则三棱锥P-SBC的体积大于 的概率是 .
的概率是 .
【答案】分析:首先分析题目,将原问题等价转化为:求△PBC的面积大于  S△ABC的概率,可借助于画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是线段的长度,再根据几何关系求解出它们的比例即可.
S△ABC的概率,可借助于画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是线段的长度,再根据几何关系求解出它们的比例即可.
解答: 解:如图,由于三棱锥P-SBC和三棱锥S-PBC的体积相等,
解:如图,由于三棱锥P-SBC和三棱锥S-PBC的体积相等,
三棱锥S-PBC与三棱锥S-ABC等高,
故在体积为V的三棱锥S-ABC的棱AB上任取一点P,三棱锥P-SBC的体积大于 ,
,
即在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于等于 即可.
即可.
记事件A={△PBC的面积大于 },
},
基本事件空间是线段AB的长度,(如图)
因为 S△PBC> ,则有
,则有  BC•PE>
BC•PE> ×
× BC•AD;
BC•AD;
化简记得到: >
> ,
,
因为PE平行AD则由三角形的相似性 >
> ;
;
 所以,事件A的几何度量为线段AP的长度,
所以,事件A的几何度量为线段AP的长度,
因为AP= AB,
AB,
所以△PBC的面积大于 S的概率=
S的概率= =
= .
.
故答案为: .
.
点评:解决有关几何概型的问题的关键是认清基本事件空间是指面积还是长度或体积,并且熟练记忆有关的概率公式.
 S△ABC的概率,可借助于画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是线段的长度,再根据几何关系求解出它们的比例即可.
S△ABC的概率,可借助于画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是线段的长度,再根据几何关系求解出它们的比例即可.解答:
 解:如图,由于三棱锥P-SBC和三棱锥S-PBC的体积相等,
解:如图,由于三棱锥P-SBC和三棱锥S-PBC的体积相等,三棱锥S-PBC与三棱锥S-ABC等高,
故在体积为V的三棱锥S-ABC的棱AB上任取一点P,三棱锥P-SBC的体积大于
 ,
,即在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于等于
 即可.
即可.记事件A={△PBC的面积大于
 },
},基本事件空间是线段AB的长度,(如图)
因为 S△PBC>
 ,则有
,则有  BC•PE>
BC•PE> ×
× BC•AD;
BC•AD;化简记得到:
 >
> ,
,因为PE平行AD则由三角形的相似性
 >
> ;
; 所以,事件A的几何度量为线段AP的长度,
所以,事件A的几何度量为线段AP的长度,因为AP=
 AB,
AB,所以△PBC的面积大于
 S的概率=
S的概率= =
= .
.故答案为:
 .
.点评:解决有关几何概型的问题的关键是认清基本事件空间是指面积还是长度或体积,并且熟练记忆有关的概率公式.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
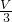 的概率是________.
的概率是________.