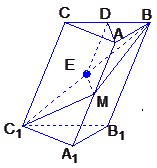
题目内容
在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．
（1）若D是BC的中点，求证： AD⊥CC1；
（2）过侧面BB1C1C的对角线BC1的平面交侧棱AA1于M，若AM=MA1，求证： 截面MBC1⊥侧面BB1C1C．
（2）过侧面BB1C1C的对角线BC1的平面交侧棱AA1于M，若AM=MA1，求证： 截面MBC1⊥侧面BB1C1C．
证明： (1) ∵AB=AC，D是BC的中点，
∴AD⊥BC
∵底面ABC⊥平面BB1C1C，
∴AD⊥侧面BB1C1C，
∴AD⊥CC1．
(2) 延长B1A1与BM交于N，连结C1N，
∵AM=MA1，
∴NA1=A1B1，
∵A1B1=A1C1，
∴A1C1=A1N=A1B1，
∴C1N⊥C1B1，
∵底面NB1C1⊥侧面BB1C1C，
∴C1N⊥侧面BB1C1C
∴截面C1NB⊥侧面BB1C1C，
∴截面MBC1⊥侧面BB1C1C．
∴AD⊥BC
∵底面ABC⊥平面BB1C1C，
∴AD⊥侧面BB1C1C，
∴AD⊥CC1．
(2) 延长B1A1与BM交于N，连结C1N，
∵AM=MA1，
∴NA1=A1B1，
∵A1B1=A1C1，
∴A1C1=A1N=A1B1，
∴C1N⊥C1B1，
∵底面NB1C1⊥侧面BB1C1C，
∴C1N⊥侧面BB1C1C
∴截面C1NB⊥侧面BB1C1C，
∴截面MBC1⊥侧面BB1C1C．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
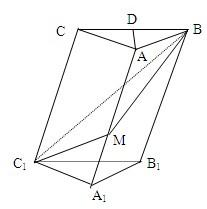在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．
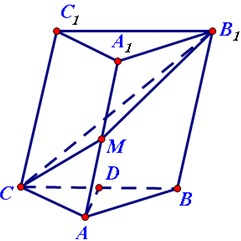在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．D为BC的中点，M为AA1的中点．
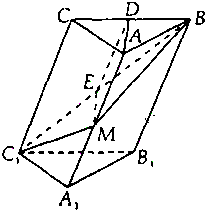在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．
