Question

（本小题满分12分）

设椭圆C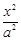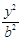：＋＝1（a＞b＞0）的左焦点为F，过点F的直线与椭圆C相交于A，B两点，直线l的倾斜角为60°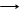，AF＝2FB.

（I）求椭圆C的离心率；

（II）如果|AB|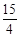＝，求椭圆C的方程.

 

Answer 1

【答案】

（I）e＝＝.

（II）椭圆C的方程为 ＋＝1

【解析】解：设A(x₁，y₁)，B(x₂，y₂)，由题意知y₁＞0，y₂＜0 .

（I）直线l的方程为 y＝(x＋c)，其中c＝，

联立得，(3a²＋b²)y²－2b²cy－3b⁴＝0，

解得 y₁＝，y₂＝ .

因为AF＝2FB，所以－y₁＝2y₂，即 ＝2·，

得离心率e＝＝.

（II）因为|AB|＝|y₂－y₁|，所以 ·＝.

由＝得b＝a，所以 a＝，得a＝3，b＝ .

所以椭圆C的方程为 ＋＝1 .