题目内容
已知定义在R上的奇函数f(x),在x∈(0,1)时,f(x)=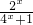 ,且f(-1)=f(1).
,且f(-1)=f(1).
(1)求f(x)在x∈[-1,1]上的解析式;
(2)证明:当x∈(0,1)时,f(x)< ;
;
(3)若x∈(0,1),常数λ∈(2, ),解关于x的不等式f(x)>
),解关于x的不等式f(x)> .
.
解:(1)∵f(x)是R上的奇函数且x∈(0,1)时,f(x)=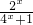 ,
,
∴当x∈(-1,0)时,f(x)=-f(-x)= =-
=-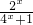 ,(1分)
,(1分)
又由于f(x)为奇函数,∴f(0)=-f(-0),∴f(0)=0,(2分)
又f(-1)=-f(1),f(-1)=f(1),∴f(-1)=f(1)=0.(3分)
综上所述,当x∈[-1,1]时,f(x)= (4分)
(4分)
(2)当x∈(0,1)时,f(x)=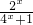 =
= ,(5分)
,(5分)
 ,当且仅当
,当且仅当 ,即x=0取等号.(6分)
,即x=0取等号.(6分)
∵x∈(0,1),∴不能取等号,
∴f(x)< ;(8分)
;(8分)
(3)λ∈(2, ),
), ∈(
∈( ,
, ),f(x)>
),f(x)> 即4x-λ•2x+1<0,
即4x-λ•2x+1<0,
设t=2x∈(1,2),不等式变为t2-λt+1<0,∵λ∈(2, ),∴△=λ2-4>0,
),∴△=λ2-4>0,
∴ <t<
<t< .(10分)
.(10分)
而当λ∈(2, )时,t>0.
)时,t>0.
综上可知,不等式的解集是(0,log2 ).(13分).
).(13分).
分析:(1)由f(x)是R上的奇函数且x∈(0,1)时,f(x)=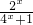 ,当x∈(-1,0)时,f(x)=-f(-x)=
,当x∈(-1,0)时,f(x)=-f(-x)= =-
=-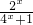 又由于f(x)为奇函数,最后写出当x∈[-1,1]时,f(x)的解析式即可;
又由于f(x)为奇函数,最后写出当x∈[-1,1]时,f(x)的解析式即可;
(2)当x∈(0,1)时,f(x)=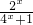 =
= 利用基本不等式即可证明得到f(x)<
利用基本不等式即可证明得到f(x)< ;
;
(3)先由λ∈(2, ),得出
),得出 ∈(
∈( ,
, ),将f(x)>
),将f(x)> 即4x-λ•2x+1<0,利用换元法设t=2x∈(1,2),不等式变为t2-λt+1<0从而解得不等式的解集即可.
即4x-λ•2x+1<0,利用换元法设t=2x∈(1,2),不等式变为t2-λt+1<0从而解得不等式的解集即可.
点评:本小题主要考查函数单调性的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
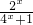 ,
,∴当x∈(-1,0)时,f(x)=-f(-x)=
 =-
=-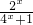 ,(1分)
,(1分)又由于f(x)为奇函数,∴f(0)=-f(-0),∴f(0)=0,(2分)
又f(-1)=-f(1),f(-1)=f(1),∴f(-1)=f(1)=0.(3分)
综上所述,当x∈[-1,1]时,f(x)=
 (4分)
(4分)(2)当x∈(0,1)时,f(x)=
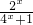 =
= ,(5分)
,(5分) ,当且仅当
,当且仅当 ,即x=0取等号.(6分)
,即x=0取等号.(6分)∵x∈(0,1),∴不能取等号,
∴f(x)<
 ;(8分)
;(8分)(3)λ∈(2,
 ),
), ∈(
∈( ,
, ),f(x)>
),f(x)> 即4x-λ•2x+1<0,
即4x-λ•2x+1<0,设t=2x∈(1,2),不等式变为t2-λt+1<0,∵λ∈(2,
 ),∴△=λ2-4>0,
),∴△=λ2-4>0,∴
 <t<
<t< .(10分)
.(10分)而当λ∈(2,
 )时,t>0.
)时,t>0.综上可知,不等式的解集是(0,log2
 ).(13分).
).(13分).分析:(1)由f(x)是R上的奇函数且x∈(0,1)时,f(x)=
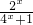 ,当x∈(-1,0)时,f(x)=-f(-x)=
,当x∈(-1,0)时,f(x)=-f(-x)= =-
=-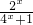 又由于f(x)为奇函数,最后写出当x∈[-1,1]时,f(x)的解析式即可;
又由于f(x)为奇函数,最后写出当x∈[-1,1]时,f(x)的解析式即可;(2)当x∈(0,1)时,f(x)=
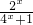 =
= 利用基本不等式即可证明得到f(x)<
利用基本不等式即可证明得到f(x)< ;
;(3)先由λ∈(2,
 ),得出
),得出 ∈(
∈( ,
, ),将f(x)>
),将f(x)> 即4x-λ•2x+1<0,利用换元法设t=2x∈(1,2),不等式变为t2-λt+1<0从而解得不等式的解集即可.
即4x-λ•2x+1<0,利用换元法设t=2x∈(1,2),不等式变为t2-λt+1<0从而解得不等式的解集即可.点评:本小题主要考查函数单调性的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)
 时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.
时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.