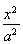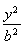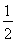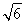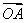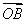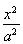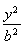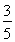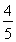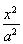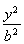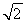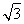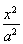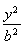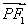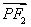题目内容
椭圆C:(1)求椭圆C的方程;
(2)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于A、B两点,且A、B关于点M对称,求直线l的方程.
解法一:(1)因为点P在椭圆C上,所以2a=|PF1|+|PF2|=6,a=3.
在Rt△PF1F2中,|F1F2|=![]() =2
=2![]() ,故椭圆的半焦距c=
,故椭圆的半焦距c=![]() ,
,
从而b2=a2-c2=4,所以椭圆C的方程为![]() =1.
=1.
(2)设A、B的坐标分别为(x1,y1),(x2,y2).
已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1),
从而可设直线l的方程为y=k(x+2)+1,
代入椭圆C的方程得(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A、B关于点M对称,所以![]() =
=![]() =-2,解得k=
=-2,解得k=![]() .
.
所以直线l的方程为y=![]() (x+2)+1,即8x-9y+25=0.
(x+2)+1,即8x-9y+25=0.
(经检验,所求直线方程符合题意)
解法二:(1)同解法一.(2)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A、B的坐标分别为(x1,y1)、(x2,y2).由题意x1≠x2且![]() =1,①
=1,①
![]() =1.②
=1.②
由①-②,得![]() =0.③
=0.③
因为A、B关于点M对称,所以x1+x2=-4,y1+y2=2.代入③得![]() ,即直线l的斜率为
,即直线l的斜率为![]() ,
,
所以直线l的方程为y-1=![]() (x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意).
(x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意).

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目