题目内容

设函数f(x)=x2+bx+c,x≤0，2,x＞0，若f(-4)=f(0),f(-2)?=-2，则方程f(x)=x的解的个数是（　　）

A．1　     B．2

C．3     D．4

解析：由已知条件求出f(x)的解析式，再解方程确定根的情况.?

由已知得.

∴f(x)=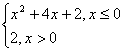

当x≤0时，方程为x2+4x+2=x, 即x2+3x+2=0,?

∴x=-1或x=-2;?

当x＞0时，方程为x=2.∴方程f(x)=x有三个解.

答案：C

练习册系列答案
相关题目
当p1，p2，…，pn均为正数时，称
n
p1+p2+…+pn
为p1，p2，…，pn的“均倒数”．已知数列{an}的各项均为正数，且其前n项的“均倒数”为
1
2n+1
．
（1）求数列{an}的通项公式；
（2）设cn=
an
2n+1
（n∈N*），试比较cn+1与cn的大小；
（3）设函数f(x)=-x2+4x-
an
2n+1
，是否存在最大的实数λ，使当x≤λ时，对于一切正整数n，都有f（x）≤0恒成立？
设函数f(x)=
x2+bx+c，(x＜0)
-x+3，(x≥0)
，且f（-4）=f（0），f（-2）=-1．
（1）求函数f（x）的解析式； 
（2）画出函数f（x）的图象，并指出函数f（x）的单调区间．
（3）若方程f（x）=k有两个不等的实数根，求k的值．
已知△ABC中，角A，B，C所对边长分别是a，b，c，设函数f(x)=x2+bx-
1
4
为偶函数，且f(cos
B
2
)=0．
（1）求角B的大小；
（2）若△ABC的面积为
3
4
，其外接圆的半径为
2
3
3
，求△ABC的周长．
设函数f(x)=
x2+bx+c，-4≤x＜0
-x+3，0≤x≤4
，且f（-4）=f（0），f（-2）=-1．
（1）求函数f（x）的解析式；
（2）画出函数f（x）的图象，并写出函数f（x）的定义域、值域．
设函数f(x)=
x2-x+n
x2+x+1
(x∈R，x≠
n-1
2
，x∈N*)，f（x）的最小值为an，最大值为bn，记cn=（1-an）（1-bn）
则数列{cn}是
常数
常数
数列．（填等比、等差、常数或其他没有规律）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网