题目内容
定义域为D的函数f(x)同时满足条件①常数a,b满足a<b,区间[a,b]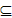 D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有
D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有
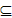 D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有
D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有 [ ]
A.1对
B.2对
C.3对
D.4对
B.2对
C.3对
D.4对
C

练习册系列答案
相关题目