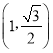题目内容
【题目】已知函数![]() ,其中a为非零常数.
,其中a为非零常数.
![]() 讨论
讨论![]() 的极值点个数,并说明理由;
的极值点个数,并说明理由;
![]() 若
若![]() ,
,![]() 证明:
证明:![]() 在区间
在区间![]() 内有且仅有1个零点;
内有且仅有1个零点;![]() 设
设![]() 为
为![]() 的极值点,
的极值点,![]() 为
为![]() 的零点且
的零点且![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)(i)证明见解析;(ii)证明见解析.
【解析】
![]() 先对函数求导,然后结合导数与单调性的关系,对a进行分类讨论即可求解函数的单调性,进而可确定极值,
先对函数求导,然后结合导数与单调性的关系,对a进行分类讨论即可求解函数的单调性,进而可确定极值,
![]() 转化为证明
转化为证明![]() 只有一个零点,结合函数与导数知识可证;
只有一个零点,结合函数与导数知识可证;
![]() 由题意可得,
由题意可得,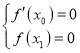 ,代入可得,
,代入可得,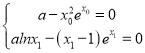 ,结合函数的性质可证.
,结合函数的性质可证.
解:![]() 解:由已知,
解:由已知,![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() ,从而
,从而![]() ,
,
所以![]() 在
在![]() 内单调递减,无极值点;
内单调递减,无极值点;
②当![]() 时,令
时,令![]() ,
,
则由于![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 上有且仅有一个极值点.
上有且仅有一个极值点.
综上所述,当![]() 时,函数
时,函数![]() 无极值点;当
无极值点;当![]() 时,函数
时,函数![]() 只有一个极值点;
只有一个极值点;
![]() 证明:
证明:![]() 由
由![]() 知
知![]() .
.
令![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 内有唯一解,从而
内有唯一解,从而![]() 在
在![]() 内有唯一解,
内有唯一解,
不妨设为![]() ,则
,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 是
是![]() 的唯一极值点.
的唯一极值点.
令![]() ,则当
,则当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 内单调递减,
内单调递减,
从而当![]() 时,
时,![]() ,所以
,所以![]() .
.
从而当![]() 时,
时,![]() ,且
,且![]()
又因为![]() ,故
,故![]() 在
在![]() 内有唯一的零点.
内有唯一的零点.
![]() 由题意,
由题意,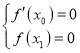 即
即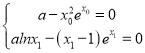 ,
,
从而![]() ,即
,即![]() .
.
因为当![]() 时,
时,![]() ,又
,又![]() ,
,
故![]() ,即
,即![]() ,
,
两边取对数,得![]() ,
,
于是![]() ,整理得
,整理得![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】截至2019年,由新华社《瞭望东方周刊》与瞭望智库共同主办的"中国最具幸福感城市"调查推选活动已连续成功举办12年,累计推选出60余座幸福城市,全国约9亿多人次参与调查,使"城市幸福感"概念深入人心.为了便于对某城市的"城市幸福感"指数进行研究,现从该市抽取若干人进行调查,绘制成如下不完整的2×2列联表(数据单位:人).
男 | 女 | 总计 | |
非常幸福 | 11 | 15 | |
比较幸福 | 9 | ||
总计 | 30 |
(1)将列联表补充完整,并据此判断是否有90%的把握认为城市幸福感指数与性别有关;
(2)若感觉"非常幸福"记2分,"比较幸福"记1分,从上表男性中随机抽取3人,记3人得分之和为![]() ,求
,求![]() 的分布列,并根据分布列求
的分布列,并根据分布列求![]() 的概率
的概率
附: ,其中
,其中![]() .
.
| 0. 10 | 0. 05 | 0. 010 | 0.001 |
| 2.706 | 3.841 | 6. 635 | 10. 828 |