Question

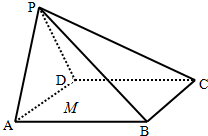（2013•营口二模）如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，M是底面正方形ABCD内的一个动点，且满足MP=MB，“△PAD是等边三角形，则点M在底面ABCD上的轨迹为（　　）

A．

B．

C．

D．

Answer 1

分析：取PB、CD、AD的中点E、F、N，连结AE、EF、AF、PN、BN．根据面面垂直的性质定理，证出PN⊥底面ABCD，正方形ABCD中证出AF⊥BN，利用三垂线定理证出AF⊥PB．等腰△PAB中，利用“三线合一”证出AE⊥PB，从而证出PB⊥平面AEF，得平面AEF是经过PB中点且与PB垂直的平面．由此结合题意可得满足条件的轨迹为平面AEF与底面ABCD的交点，得到本题答案．

解答：解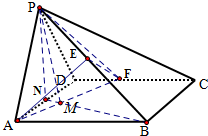：取PB、CD、AD的中点E、F、N，连结AE、EF、AF、PN、BN
∵等边△PAD中，N是AD中点，∴PN⊥AD
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴PN⊥底面ABCD，可得BN是PB在底面ABCD内的射影
∵正方形ABCD中，F、N分别为CD、AD的中点
∴Rt△ADF≌△BAN，可得AF⊥BN
由此可得AF⊥PB
又∵△PAB中，PA=AB，E为PB中点，∴AE⊥PB
结合AE、AF是平面AEF内的相交直线，得到PB⊥平面AEF
平面AEF∩底面ABCD=AF，
由于平面AEF是经过PB中点且与PB垂直的平面，可得平面AEF内的任意一点到P、B两点的距离相等
∴满足题意的点M在平面AEF内，可得点M在底面ABCD上的轨迹为线段AF
故选：B

点评：本题给出特殊的四棱锥，求动点M的轨迹．着重考查了空间面面垂直的性质、线面垂直的判定与性质、正方形和等腰三角形的性质等知识，属于中档题．