题目内容
关于x的方程x2-|x|-k2=0，下列判断：
①存在实数k，使得方程有两个不同的实数根；
②存在实数k，使得方程有三个不同的实数根；
③存在实数k，使得方程有四个不同的实数根．
其中正确的有________（填相应的序号）．
①②
分析：将方程x2-|x|-k2=0的问题转化成函数y=x2-|x|与函数y=k2图象的交点问题，画出图象可得．
解答：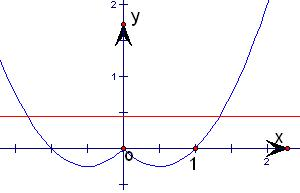
解：关于x的方程x2-|x|-k2=0，可化为x2-|x|=k2
分别画出函数y=x2-|x|和y=k2的图象，如图．
由图可知，它们的交点情况是：
恰有2，3个不同的交点
故答案为：①②．
点评：本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想．
分析：将方程x2-|x|-k2=0的问题转化成函数y=x2-|x|与函数y=k2图象的交点问题，画出图象可得．
解答：
解：关于x的方程x2-|x|-k2=0，可化为x2-|x|=k2分别画出函数y=x2-|x|和y=k2的图象，如图．
由图可知，它们的交点情况是：
恰有2，3个不同的交点
故答案为：①②．
点评：本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想．
练习册系列答案
阅读快车系列答案
相关题目