题目内容
已知函数 .
.(1)试判断直线
 是否是函数f(x)图象的对称轴,并说明理由;
是否是函数f(x)图象的对称轴,并说明理由;(2)在△ABC中,若
 ,求边AC的长.
,求边AC的长.
【答案】分析:(1)把f(x)利用诱导公式,二倍角的正弦、余弦公式及特殊角的三角函数值化简得到一个角的正弦函数,代入 函数是否取得最值,即可判断函数是否关于
函数是否取得最值,即可判断函数是否关于 对称;
对称;
(2)根据f(A)=1利用同角三角函数间的基本关系化简得到sinA=cosA即A= ,然后根据正弦定理即可求出AC的值.
,然后根据正弦定理即可求出AC的值.
解答:解:(1)由 得到:
得到:
f(x)=cos2x+sinxcosx= +
+
= (
(  cos2x+
cos2x+ sin2x)+
sin2x)+ =
= ,
,
∴ 时函数f(x)取得最大值,所以直线
时函数f(x)取得最大值,所以直线 是函数f(x)图象的对称轴;
是函数f(x)图象的对称轴;
(2)∵f(A)=cos2A+sinAcosA=1
移项得:sinAcosA=1-cos2A=sin2A,因为A为锐角,所以sinA≠0
∴sinA=cosA,则
根据正弦定理得: =
= 即
即  =
= ,
,
所以AC= =
= .
.
点评:考查学生灵活运用诱导公式、二倍角公式、同角三角函数间的基本关系及特殊角的三角函数值化简求值,会利用正弦定理解决实际问题.
 函数是否取得最值,即可判断函数是否关于
函数是否取得最值,即可判断函数是否关于 对称;
对称;(2)根据f(A)=1利用同角三角函数间的基本关系化简得到sinA=cosA即A=
 ,然后根据正弦定理即可求出AC的值.
,然后根据正弦定理即可求出AC的值.解答:解:(1)由
 得到:
得到:f(x)=cos2x+sinxcosx=
 +
+
=
 (
(  cos2x+
cos2x+ sin2x)+
sin2x)+ =
= ,
,∴
 时函数f(x)取得最大值,所以直线
时函数f(x)取得最大值,所以直线 是函数f(x)图象的对称轴;
是函数f(x)图象的对称轴;(2)∵f(A)=cos2A+sinAcosA=1
移项得:sinAcosA=1-cos2A=sin2A,因为A为锐角,所以sinA≠0
∴sinA=cosA,则

根据正弦定理得:
 =
= 即
即  =
= ,
,所以AC=
 =
= .
.点评:考查学生灵活运用诱导公式、二倍角公式、同角三角函数间的基本关系及特殊角的三角函数值化简求值,会利用正弦定理解决实际问题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目

 (理)已知函数
(理)已知函数
 (理)已知函数
(理)已知函数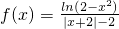 .
.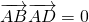 ,求D2+E2-4F的值;
,求D2+E2-4F的值; .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;
