Question

设x_i∈［1,+∞)(i=1,2,…,n)，

求证：.

Answer 1

证明：①先证明n=2^m(m∈N)原不等式恒成立，

（A）m=0时原不等式显然成立，m=1时,

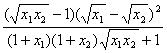=≥0，

∴此时原不等式成立.

（B）设m=k即n=2^k时原不等式成立，令2^k=p，

则x_i∈［1,+∞)(i=1,2,…,p)时，

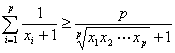恒成立.

则x_i∈［1,+∞)(i=1,2,…,2p)时，

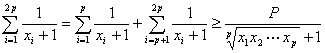
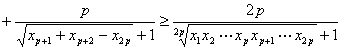
即n=2p=2^k+1,m=k+1时原不等式成立.

由（A）（B）可知对于任何m∈N,n=2^m时原不等式成立.

②对于任何n∈N^*,必存在k,使p=2^k＞n成立.

令x_n+1=x_n+2=…=x_p

=，

则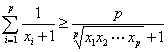成立，

即.

∴成立.

由①②可知对于任何n∈N^*,

成立.