题目内容
 △ABC中,角A,B,C的对边a,b,c,
△ABC中,角A,B,C的对边a,b,c, ,△ABC外接圆半径为1.
,△ABC外接圆半径为1.
(1)若a+c=3,求a及c边.
(2)若BC中点为D, ,
, ,求△ABC面积.
,求△ABC面积.
解:(1)∵ =2R=2,
=2R=2,
∴ =
= (2分)
(2分)
∴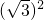 =
=
∴3=(a+c)2-3ac,∴ac=2 (4分)
由 ,可得
,可得 或
或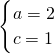 (6分)
(6分)
(2)△ABD与△ACD中 =
= ,
, =
= (8分)
(8分)
∵∠DAC= ,∠B=
,∠B= ,∴
,∴
又BD=CD,∴ ,∴
,∴ (10分)
(10分)
∴ 或
或
又 ,∴
,∴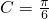 ,∴△ABC为直角三角形,∴
,∴△ABC为直角三角形,∴ (12分)
(12分)
分析:(1)利用正弦定理可求b,再利用余弦定理及a+c=3,建立方程组,即可求a及c边.
(2)先求C,并求得△ABC为直角三角形,即可求△ABC面积.
点评:本题考查余弦定理、正弦定理的运用,考查学生的计算能力,属于中档题.
 =2R=2,
=2R=2,
∴
 =
= (2分)
(2分)∴
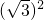 =
=
∴3=(a+c)2-3ac,∴ac=2 (4分)
由
 ,可得
,可得 或
或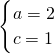 (6分)
(6分)(2)△ABD与△ACD中
 =
= ,
, =
= (8分)
(8分)∵∠DAC=
 ,∠B=
,∠B= ,∴
,∴
又BD=CD,∴
 ,∴
,∴ (10分)
(10分)∴
 或
或
又
 ,∴
,∴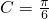 ,∴△ABC为直角三角形,∴
,∴△ABC为直角三角形,∴ (12分)
(12分)分析:(1)利用正弦定理可求b,再利用余弦定理及a+c=3,建立方程组,即可求a及c边.
(2)先求C,并求得△ABC为直角三角形,即可求△ABC面积.
点评:本题考查余弦定理、正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目