题目内容
【题目】在直角坐标系
中，直线
与抛物线
交于
，
两点，且
.
（1）求
的方程；
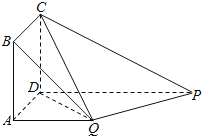
（2）试问：在
轴的正半轴上是否存在一点
，使得
的外心在上？若存在，求的坐标；若不存在，请说明理由..
【答案】（1）
； （2）在
轴的正半轴上存在一点
，使得
的外心在
上.
【解析】
（1）联立
，得
，利用
，结合韦达定理列方程求得
，从而可得结果；（2）求出线段
的中垂线方程
.联立
，得
，解得
或
，从而
的外心
的坐标为
或
，分别利用
求得
的值，验证是否符合题意即可.
（1）联立，得，
则
，
，
从而
.
，
，
即
，解得，故的方程为.
（2）设线段的中点为
，
由（1）知，
，
，
则线段的中垂线方程为
，即.
联立，得，解得或，
从而的外心的坐标为或.
假设存在点
，设的坐标为，
，
，则
.
，
.
若的坐标为，则
，
，则的坐标不可能为.
故在轴的正半轴上存在一点，使得的外心在上.
练习册系列答案
相关题目
【题目】2018年，南昌市召开了全球VR产业大会，为了增强对青少年VR知识的普及，某中学举行了一次普及VR知识讲座，并从参加讲座的男生中随机抽取了50人，女生中随机抽取了70人参加VR知识测试，成绩分成优秀和非优秀两类，统计两类成绩人数得到如下的列联表：
优秀 | 非优秀 | 总计 | |
男生 | a | 35 | 50 |
女生 | 30 | d | 70 |
总计 | 45 | 75 | 120 |
（1）确定a,d的值；
（2）试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关；
（3）为了宣传普及VR知识，从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法，随机选出6名组成宣传普及小组．现从这6人中随机抽取2名到校外宣传，求“到校外宣传的2名同学中至少有1名是男生”的概率.
附：
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
