题目内容
三棱锥A-BCD中，AB=AC=BC=CD=AD=a，要使三棱锥A-BCD的体积最大，则二面角B-AC-D的大小为（ ）A．
B．
C．
D．
【答案】分析：因为△ACD为边长为a的正三角形，故三棱锥A-BCD的体积最大问题转化为点B到平面BCD的距离最大问题，三棱之中，高≤斜高，可求出高的最大值，从而确定三棱锥，求解二面角B-AC-D即可．
解答：解：因为△ACD为边长为a的正三角形，要使三棱锥B-ACD的体积最大，则三棱锥B-ACD的高最大，
因为△ABC为边长为a的正三角形，高为
，
而三棱锥B-ACD的高小于等于
，
故三棱锥B-ACD的高最大值为
，
此时面ABC⊥面ACD，所以二面角B-AC-D的大小为
故选A．
点评：本题考查三棱锥的体积问题，在三棱锥中，任何一个面都可以作为底面．考查空间想象能力和转化思想．
解答：解：因为△ACD为边长为a的正三角形，要使三棱锥B-ACD的体积最大，则三棱锥B-ACD的高最大，
因为△ABC为边长为a的正三角形，高为
，而三棱锥B-ACD的高小于等于
，故三棱锥B-ACD的高最大值为
，此时面ABC⊥面ACD，所以二面角B-AC-D的大小为
故选A．
点评：本题考查三棱锥的体积问题，在三棱锥中，任何一个面都可以作为底面．考查空间想象能力和转化思想．
练习册系列答案
相关题目
如图，在三棱锥A-BCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．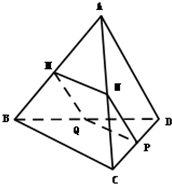
如图，在三棱锥A-BCD中，平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点，且MN=PQ．