题目内容
球的表面积与它的内接正方体的表面积之比是（ ）
A． | B． | C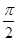． | D． |
C
解析试题分析：设球的半径为
，则球的表面积为
,而球的内接正方体的体对角线等于球的直径，所以正方体的棱长为
，所以球的表面积和内接正方体的表面积之比为
考点：本小题主要考查球的表面积公式、正方体的表面积公式的应用和球与其内接正方体的关系，考查学生的空间想象能力.
点评：正方体内接于球，则球的直径等于正方体的体对角线；若球内切于正方体，则球的直径等于正方体的棱长.
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
设有一几何体的三视图如下，则该几何体体积为（ ）
正视图 侧视图
俯视图（圆和正方形）
A．4+ | B．4+ | C．4+ | D．4+ |
一个棱锥的三视图如图，则该棱锥的全面积（单位：cm2）为( ) 
A．36+12 | B．48+24 | C．48+12 | D．36+24 |
正方体的棱长为
，由它的互不相邻的四个顶点连线所构成的四面体的体积是（ ）
A． | B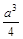． | C． | D． |
正三棱柱
的各棱长都是2，E，F分别是
的中点，则EF的长是（ ）
| A．2 | B． | C． | D． |
则
的形状是( )
正三角形 
等腰三角形 
直角三角形 
其他类型