Question

已知函数为常数，e=2.71828…是自然对数的底数)，曲线在点处的切线与x轴平行.

(Ⅰ)求k的值；

(Ⅱ)求的单调区间；

(Ⅲ)设，其中为的导函数.证明：对任意.[来源:学科网ZXXK]

Answer 1

I)，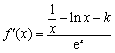

由已知，，∴.

(II)由(I)知，.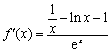

设，则，即在上是减函数，

由知，当时，从而，

当时，从而.

综上可知，的单调递增区间是，单调递减区间是.

(III)由(II)可知，当时，≤0＜1+，故只需证明在时成立.

当时，＞1，且，∴.

设，，则，

当时，，当时，，

所以当时，取得最大值.

所以.

综上，对任意，.

[来源:学,科,网]