题目内容
已知函数f(x)=kx,g(x)= .
.
(1)若不等式f(x)=g(x)在区间 (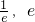 )内的解的个数;
)内的解的个数;
(2)求证: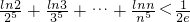 .
.
解:(Ⅰ)由f(x)=g(x),得 .
.
令 所以,方程f(x)=g(x),在区间
所以,方程f(x)=g(x),在区间 内解的个数即为函数
内解的个数即为函数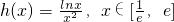 的图象与直线y=k交点的个数.
的图象与直线y=k交点的个数.
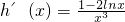 当h′(x)=0时,x=
当h′(x)=0时,x= .
.
当x在区间 内变化时,h′(x),h(x)变化如下:
内变化时,h′(x),h(x)变化如下:
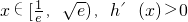 ;
;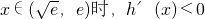
当 时,y=-e2;当
时,y=-e2;当 时,
时,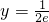 ;当x=e时,
;当x=e时,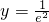 .
.
所以,(1)当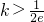 或k<-e2时,该方程无解
或k<-e2时,该方程无解
(2)当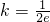 或
或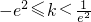 时,该方程有一个解;
时,该方程有一个解;
(3)当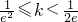 时,该方程有两个解.
时,该方程有两个解.
(Ⅱ)由(Ⅰ)知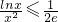 ,
,
∴ .
.
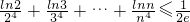
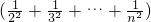
∴∴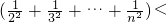
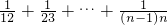
=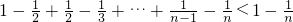 <1
<1
∴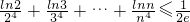
∵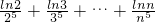
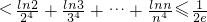
∴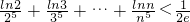 .
.
分析:(I)将方程的解的个数问题转化为函数的图象的交点个数问题;通过导数研究函数的单调性及极值;通过对k与函数h(x)的极值的大小关系的讨论得到方程解的情况.
(II)通过(I)得到的函数的单调性,通过对不等式放缩,利用数列的裂项求和的方法证出不等式.
点评:本题考查通过导函数研究函数的单调性、求函数的极值、求函数交点的个数,以及通过放缩的方法证明不等式、考查利用裂项法求数列的和.
 .
.令
 所以,方程f(x)=g(x),在区间
所以,方程f(x)=g(x),在区间 内解的个数即为函数
内解的个数即为函数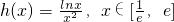 的图象与直线y=k交点的个数.
的图象与直线y=k交点的个数.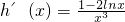 当h′(x)=0时,x=
当h′(x)=0时,x= .
.当x在区间
 内变化时,h′(x),h(x)变化如下:
内变化时,h′(x),h(x)变化如下: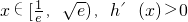 ;
;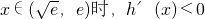
当
 时,y=-e2;当
时,y=-e2;当 时,
时,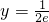 ;当x=e时,
;当x=e时,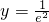 .
.所以,(1)当
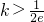 或k<-e2时,该方程无解
或k<-e2时,该方程无解(2)当
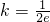 或
或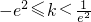 时,该方程有一个解;
时,该方程有一个解;(3)当
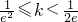 时,该方程有两个解.
时,该方程有两个解.(Ⅱ)由(Ⅰ)知
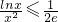 ,
,∴
 .
.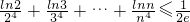
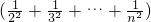
∴∴
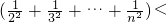
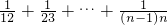
=
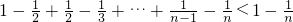 <1
<1∴
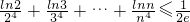
∵
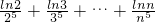
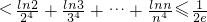
∴
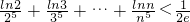 .
.分析:(I)将方程的解的个数问题转化为函数的图象的交点个数问题;通过导数研究函数的单调性及极值;通过对k与函数h(x)的极值的大小关系的讨论得到方程解的情况.
(II)通过(I)得到的函数的单调性,通过对不等式放缩,利用数列的裂项求和的方法证出不等式.
点评:本题考查通过导函数研究函数的单调性、求函数的极值、求函数交点的个数,以及通过放缩的方法证明不等式、考查利用裂项法求数列的和.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目