题目内容
已知命p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
| 1 |
| x |
| A．命题“p∧q”是真命题 | B．命题“（￢p）∧q”是真命题 |
| C．命题“p∧（￢q）”是真命题 | D．命题“（￢p）∧（￢q）”是真命题 |
∵命p：?x∈R，使得x+
＜2，解这个不等式的x＜0，
∴存在x∈R，使得x+
＜2，故本命题正确，
命题q：?x∈R，x2+x+1＞0，
∵x2+x+1＞0等价于(x+
)2+
＞0
∴?x∈R，x2+x+1＞0，正确，
所给的两个命题都正确，
∴命题“p∧q”是真命题
故选A．
| 1 |
| x |
∴存在x∈R，使得x+
| 1 |
| x |
命题q：?x∈R，x2+x+1＞0，
∵x2+x+1＞0等价于(x+
| 1 |
| 2 |
| 3 |
| 4 |
∴?x∈R，x2+x+1＞0，正确，
所给的两个命题都正确，
∴命题“p∧q”是真命题
故选A．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知命p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“（￢p）∧q”是真命题 |
| C、命题“p∧（￢q）”是真命题 |
| D、命题“（￢p）∧（￢q）”是真命题 |
，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）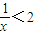
，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
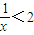，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）