题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,S是该三角形的面积.
(1)若 ,
, ,
, ,求角B的度数;
,求角B的度数;
(2)若a=8, ,
, ,求b的值.
,求b的值.
解:(1)∵ ,
, ,
, ,
,
∴4cosB•sin2 +cos2B=0,
+cos2B=0,
∴4cosB•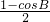 +2cos2B-1=0,
+2cos2B-1=0,
∴cosB= ,
,
∵∠B∈(0,180°),
∴∠B=60°;…(6分)
(2)∵S=8 ,
,
∴ acsinB=8
acsinB=8 ,…(7分)
,…(7分)
又a=8,B= ,
,
∴c=4,…(8分)
由余弦定理得:b2=a2+c2-2accosB=82+42-2•8•4cos120°=112,…(10分)
则b=4 .…(12分)
.…(12分)
分析:(1)由两向量的坐标及两向量平行,根据平面向量的数量积法则列出关系式,再利用二倍角的余弦函数公式化简,整理后得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)由B的度数求出sinB的值,再由a,已知三角形的面积S,利用三角形的面积公式求出c的值,再由a,c及cosB的值,利用余弦定理即可求出b的值.
点评:此题考查了平面向量的数量积运算,余弦定理,三角形的面积公式,二倍角的余弦函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.
 ,
, ,
, ,
,∴4cosB•sin2
 +cos2B=0,
+cos2B=0,∴4cosB•
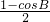 +2cos2B-1=0,
+2cos2B-1=0,∴cosB=
 ,
,∵∠B∈(0,180°),
∴∠B=60°;…(6分)
(2)∵S=8
 ,
,∴
 acsinB=8
acsinB=8 ,…(7分)
,…(7分)又a=8,B=
 ,
,∴c=4,…(8分)
由余弦定理得:b2=a2+c2-2accosB=82+42-2•8•4cos120°=112,…(10分)
则b=4
 .…(12分)
.…(12分)分析:(1)由两向量的坐标及两向量平行,根据平面向量的数量积法则列出关系式,再利用二倍角的余弦函数公式化简,整理后得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)由B的度数求出sinB的值,再由a,已知三角形的面积S,利用三角形的面积公式求出c的值,再由a,c及cosB的值,利用余弦定理即可求出b的值.
点评:此题考查了平面向量的数量积运算,余弦定理,三角形的面积公式,二倍角的余弦函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |