题目内容
如图，正四棱锥S—ABCD中，E是侧棱SC的中点，异面直线SA和BC所成角的大小是60°.(1)求证：直线SA∥平面BDE；
(2)求二面角ASBD的大小；
(3)求直线BD和平面SBC所成角的大小.
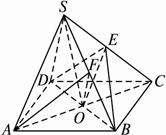
解法一:(1)证明：连结AC交BD于点O，连结OE，因为S—ABCD是正四棱锥，?
所以四边形ABCD是正方形.所以O是AC的中点.?
因为E是侧棱SC的中点，所以OE∥AS. ?
又OE
平面BDE，AS
平面BDE，所以直线SA∥平面BDE.
?
(2)解：因为AD∥BC，异面直线SA和BC所成角的大小是60°，?
所以∠SAD=60°. ?
△SDA是等边三角形.?
根据正棱锥的性质得，△SDC、△SBA、△SBC也是等边三角形.?
连结SO，取SB中点F，连结AF、OF，?
因为O是正方形ABCD的中心，根据正棱锥的性质得，SO⊥平面ABCD，?
所以AO⊥SO.又AO⊥BD，所以AO⊥平面SBD. ?
所以OF是AF在平面SBD上的射影.?
因为SB⊥AF，?
根据三垂线定理的逆定理,得OF⊥SB，?
所以∠AFO是二面角A-SB-D的平面角. ?
因为OA=
AB=
SD=
OF，?
所以在Rt△AOF中，tan∠AFO=
=
,?
即二面角A-SB-D的大小是arctan
. ?
(3)解：因为E是侧棱SC的中点，所以BE⊥SC，DE⊥SC.?
所以SC⊥平面BDE.所以平面SCB⊥平面BDE.?
过D作平面SCB的垂线，垂足在直线BE上，?
即BE为BD在平面SCB上的射影.?
所以∠DBE为直线BD和平面SBC所成的角. ?
因为OB=
AB，BE=
AB，所以cOS∠DBE=
=
.?
所以直线BD和平面SBC所成的角的大小为arccos
. ?
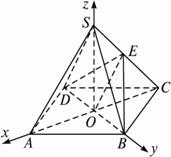
解法二:(1)证明：连结AC交BD于点O，连结SO,OE.?
根据正四棱锥的性质得SO⊥面ABCD.?
以OA、OB、OS所在射线分别作为非负x轴、非负y轴、非负z轴建立空间直角坐标系.
因为异面直线SA和BC所成角的大小是60°，AD∥BC，??
所以∠SAD=60°. ?
因而△SDA是等边三角形.??
根据正棱锥的性质，得△SDC,△SBA,△SBC也是等边三角形.?
设AB=a，则A(
a,0,0),S(0,0,
a),E(-
a,0,
a),B(0,
a,0).?
因为
=(-
a，0,
a)，
=(-
a，0，
a)，?
所以
=2
.?所以AS∥OE. ?
又OE
面BDE，AS
面BDE，?
所以AS∥面BDE.
?
(2)解:设n1=(x1,y1,z1)是平面SAB的法向量.?
则由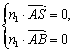
得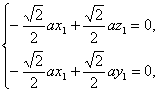
?
取x1=1,得n1=(1，1，1). ?
因为OA⊥SO，且OA⊥BD，所以
是平面SBD的法向量.?
则cos〈n,
〉=
=
. ?
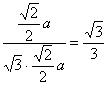所以二面角ASBD的大小是arccos
. ?
(3)解:设n2=(x2,y2,z2)是平面SBC的法向量.?
则由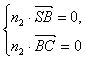
得
取x2=1,得n2=(1，-1，-1),
又
=(0，-
a,0),?
则cos〈
，n2〉=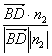
=
=
. ?
设BD和平面SBC所成角的大小为α，则sinα=
,??
即直线BD和平面SBC所成的角为arcsin
.
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
如图，正四棱锥S-ABCD中，E是侧棱SC的中点，异面直线SA和BC所成角的大小是60°．
12、如图在正四棱锥S-ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC，则动点P的轨迹与△SCD组成的相关图形是（ ）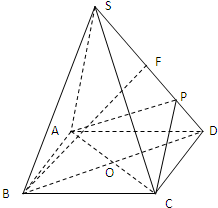
如图，正四棱锥S-ABCD 的底面是边长为a正方形，O为底面对角线交点，侧棱长是底面边长的
（2006•西城区二模）如图，正四棱锥S-ABCD中，E是侧棱SC的中点，异面直线SA和BC所成角的