题目内容
17.某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行观测研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(Ⅱ)请根据4月7日、4月15日、4月21日三天的数据,求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,若选取的是4月1日与4月30日的两组数据作为检验数据,试问(Ⅱ)中所得的线性回归方程是否可靠?
参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$;
参考数据:11×25+13×30+12×26=977,112+132+122=434.
分析 (I)列出(m,n)的所有取值情况,设“m、n均不小于25”为事件A,找出事件A包含的基本事件个数,即可求解事件A的概率.
(II)求出y关于x的线性回归方程的相关数值即可.
(III)通过x=10时,x=8时,计算估计数据,然后判断线性回归方程是否可靠.
解答 解:(I)(m,n)的所有取值情况有
(23,25),(23,30),(23,26),(23,16),(25,30)(25,26),(25,16),(30,26),(30,16),(26,16),
共有10个,…(2分)
设“m、n均不小于25”为事件A,则事件A包含的基本事件有
(25,30),(25,26)(30,26),
∴$P(A)=\frac{3}{10}$,故事件A的概率为$\frac{3}{10}$;…(4分)
(II)由数据得$\overline x=12,\overline y=27$,$3\overline x\overline y=972$,$3{\overline x^2}=432$,
又$\sum_{i=1}^3{{x_i}{y_i}}=977$,$\sum_{i=1}^3{{x_i}^2}=434$,∴$\hat b=\frac{977-972}{434-432}=\frac{5}{2}$,$\hat a=27-\frac{5}{2}×12=-3$.
∴y关于x的线性回归方程为$\hat y=\frac{5}{2}x-3$;…(8分)
(III)当x=10时,$\hat y=22$,|22-23|<2,当x=8时,$\hat y=17$,|17-16|<2,
∴得到的线性回归方程是可靠的.…(12分)
点评 本题考查概率的求法,回归直线方程的求法,考查计算能力.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
12.已知函数f(x)=-2x-1+$\frac{1}{{{2^{x+1}}}}$,g(x)=x3-3x,那么函数y=f(g(x))是( )
| A. | 奇函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| B. | 奇函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 | |
| C. | 偶函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| D. | 偶函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 |
 已知一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )
已知一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )



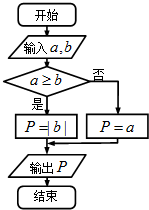 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( ) 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数 的图象,则函数
的图象,则函数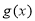 的单调递减区间是( )
的单调递减区间是( ) B.
B.
 D.
D.