题目内容
在平面直角坐标系xOy中，点A（-1，-2）、B（2，3）、C（-2，-1）．设实数t满足（
-t
）•=0，则t的值=________．
-
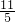
分析：利用向量的坐标公式求出
，=（-2，-1），将它们代入已知向量的等式，利用向量的数量积公式得到关于t的方程，求出t的值．
解答：由题设知：，=（-2，-1），
．
由（
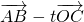）•=0，得：
（3+2t，5+t）•（-2，-1）=0，
从而5t=-11，
所以
．
故答案为：
．
点评：本题考查向量的坐标的求法以及向量的数量积公式，是一道基础题，对公式要求熟记．
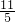
分析：利用向量的坐标公式求出
，=（-2，-1），将它们代入已知向量的等式，利用向量的数量积公式得到关于t的方程，求出t的值．解答：由题设知：
，=（-2，-1），．由（
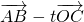）•=0，得：（3+2t，5+t）•（-2，-1）=0，
从而5t=-11，
所以
．故答案为：
．点评：本题考查向量的坐标的求法以及向量的数量积公式，是一道基础题，对公式要求熟记．
练习册系列答案
一线名师提优试卷系列答案
相关题目
在平面直角坐标系xOy中，双曲线中心在原点，焦点在y轴上，一条渐近线方程为x-2y=0，则它的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．