题目内容
试构造出一个三棱锥S-ABC,使其四个面中成直角三角形的个数最多,作出图形,指出所有的直角,并证明你的结论.
分析:SA⊥平面ABC,∠ABC=90°,则∠SAC=∠SAB=90°,由此能求出∠SBC=90°,即四个面SAB,SAC,SBC,ABC为直角三角形.
解答:解:如图,SA⊥平面ABC,∠ABC=90°,
则∠SAC=∠SAB=90°,
又AB⊥BC,所以BC⊥SB,
所以∠SBC=90°,
即四个面SAB,SAC,SBC,ABC为直角三角形.
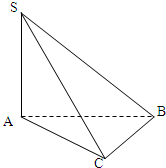
则∠SAC=∠SAB=90°,
又AB⊥BC,所以BC⊥SB,
所以∠SBC=90°,
即四个面SAB,SAC,SBC,ABC为直角三角形.

点评:本题考查棱锥的结构特征,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目