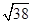题目内容
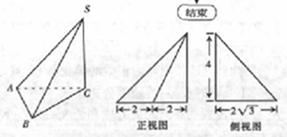
如图所示,在四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形,

 ,
, 

 ,侧棱
,侧棱
 底面
底面 ,且
,且 ,则点
,则点 到平面
到平面 的距离为( )
的距离为( )
A. | B. |
C. | D. |
D
解析试题分析:由侧棱
 底面
底面 可知,
可知, ,连接BD,
,连接BD, ,则
,则 .连接AC,直角梯形中,可得
.连接AC,直角梯形中,可得 ,
, 。侧棱
。侧棱
 底面
底面 ,所以侧棱
,所以侧棱
 AC,直角三角形SAC中,
AC,直角三角形SAC中, ,直角三角形ACD中
,直角三角形ACD中 ,
, 中,由余弦定理可得
中,由余弦定理可得 ,则
,则 ,
, .所以
.所以 即
即
 .
.
考点:几何体的体积,等积法求点到面的距离.

练习册系列答案
相关题目
一个正三棱柱的三视图如图所示,这个三棱柱的侧(左)视图的面积为 ,则这个三棱柱的体积为 ( )
,则这个三棱柱的体积为 ( )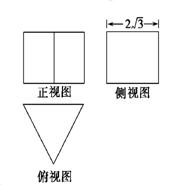
| A.12 | B.16 | C.8 | D.12 |
个棱锥的三视图如上图,则该棱锥的全面积(单位:cm2)为( )
A.48+12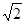 | B.48+24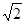 | C.36+12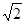 | D.36+24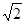 |
如图,在棱长为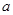 的正方体
的正方体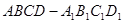 中,
中,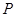 为
为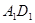 的中点,
的中点, 为
为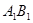 上任意一点,
上任意一点,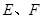 为
为 上任意两点,且
上任意两点,且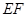 的长为定值,则下面四个值中不为定值的是
的长为定值,则下面四个值中不为定值的是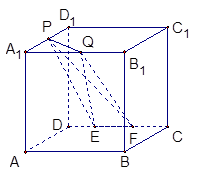
A.点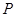 到平面 到平面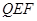 的距离 的距离 |
B.直线 与平面 与平面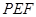 所成的角 所成的角 |
C.三棱锥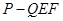 的体积 的体积 |
D.二面角 的大小 的大小 |
某几何体的三视图如图所示,该几何体的体积是( ) 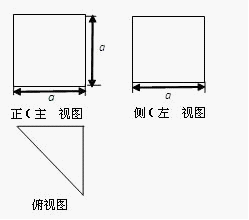
A. |
B. |
C.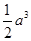 |
D.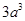 |
如图,正方体的底面与正四面体的底面在同一平面 上,且
上,且 ,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为
,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为 ,那么
,那么 ( )
( )
| A.8 |
| B.9 |
| C.10 |
| D.11 |




 ;直径为2的球的体积为
;直径为2的球的体积为 .则
.则 ( )
( )