题目内容
从正方体的12条棱中选出k条，使得其中任意两条线段所在的直线都是异面直线，则k的最大值是（ ）
分析：根据正方体的结构特征，从上底面的4条棱中最多选出一条，从4条侧棱中最多选一条，从下底面的4条棱中最多选一条，从而确定k的最大值．
解答：解：由于正方体上底面的4条棱共面，4条侧棱互相平行，下底面的4条棱共面，
从正方体的12条棱中选出k条，使得其中任意两条线段所在的直线都是异面直线，
则应从上底面的4条棱中最多选出一条，从4条侧棱中最多选一条，从下底面的4条棱中最多选一条，
故k的最大值为3，
故选A．
从正方体的12条棱中选出k条，使得其中任意两条线段所在的直线都是异面直线，
则应从上底面的4条棱中最多选出一条，从4条侧棱中最多选一条，从下底面的4条棱中最多选一条，
故k的最大值为3，
故选A．
点评：本题考查异面直线的判定，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
习题精选系列答案
相关题目
为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,
;当两条棱平行时,
.
;
.
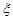为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，
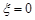；当两条棱平行时，
．
；
．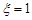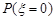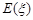