题目内容
已知函数f(x)=4x3+3tx2-6t2x+t-1,其中t>0.
(1)求f(x)的单调区间;
(2)证明:对任意的t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
(1)f'(x)=12x2+6tx-6t2,令f′(x)=0,得x=-t或x= .
.
∵t>0,∴ ,
,
当x变化时,f'(x),f(x)的变化情况如下表:
∴f(x)的单调递增区间是(-∞,-t),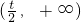 ,f(x)的单调递减区间是
,f(x)的单调递减区间是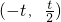 .
.
(2)证明:由(1)可知,当t>0时,f(x)在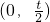 内单调递减,在
内单调递减,在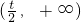 内单调递增,以下分两种情况讨论:
内单调递增,以下分两种情况讨论:
①当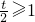 ,即t≥2时,f(x)在(0,1)内单调递减,f(0)=t-1>0,f(1)=-6t2+4t+3≤-6×4+4×2+3<0.
,即t≥2时,f(x)在(0,1)内单调递减,f(0)=t-1>0,f(1)=-6t2+4t+3≤-6×4+4×2+3<0.
所以对任意t∈[2,+∞),f(x)在区间(0,1)内均存在零点.
②当 ,即0<t<2时,f(x)在
,即0<t<2时,f(x)在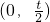 内单调递减,在
内单调递减,在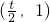 内单调递增,
内单调递增,
若t∈(0,1], ,f(1)=-6t2+4t+3≥-6t+4t+3=3-2t>0,所以f(x)在
,f(1)=-6t2+4t+3≥-6t+4t+3=3-2t>0,所以f(x)在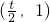 内存在零点.
内存在零点.
若t∈(1,2), ,f(0)=t-1>0,所以f(x)在
,f(0)=t-1>0,所以f(x)在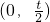 内存在零点.
内存在零点.
所以,对任意t∈(0,2),f(x)在区间(0,1)内均存在零点.
综上,对任意t∈(0,+∞)在区间(0,1)内均存在零点.
分析:(1)求出f′(x),解方程f′(x)=0,以表格表示当x变化时,f'(x),f(x)的变化情况,由表格即可求出单调区间;
(2)借助(1)问的结论,按照函数零点的存在条件,分情况进行讨论,可证明.
点评:本题考查函数的零点存在条件以及利用导数研究函数的单调性问题,本题中渗透了分类讨论思想.
 .
.∵t>0,∴
 ,
,当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-t) | 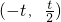 | 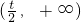 |
| f'(x) | + | - | + |
| f(x) | ↗ | ↘ | ↗ |
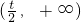 ,f(x)的单调递减区间是
,f(x)的单调递减区间是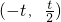 .
.(2)证明:由(1)可知,当t>0时,f(x)在
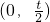 内单调递减,在
内单调递减,在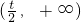 内单调递增,以下分两种情况讨论:
内单调递增,以下分两种情况讨论:①当
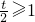 ,即t≥2时,f(x)在(0,1)内单调递减,f(0)=t-1>0,f(1)=-6t2+4t+3≤-6×4+4×2+3<0.
,即t≥2时,f(x)在(0,1)内单调递减,f(0)=t-1>0,f(1)=-6t2+4t+3≤-6×4+4×2+3<0.所以对任意t∈[2,+∞),f(x)在区间(0,1)内均存在零点.
②当
 ,即0<t<2时,f(x)在
,即0<t<2时,f(x)在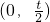 内单调递减,在
内单调递减,在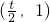 内单调递增,
内单调递增,若t∈(0,1],
 ,f(1)=-6t2+4t+3≥-6t+4t+3=3-2t>0,所以f(x)在
,f(1)=-6t2+4t+3≥-6t+4t+3=3-2t>0,所以f(x)在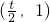 内存在零点.
内存在零点.若t∈(1,2),
 ,f(0)=t-1>0,所以f(x)在
,f(0)=t-1>0,所以f(x)在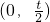 内存在零点.
内存在零点.所以,对任意t∈(0,2),f(x)在区间(0,1)内均存在零点.
综上,对任意t∈(0,+∞)在区间(0,1)内均存在零点.
分析:(1)求出f′(x),解方程f′(x)=0,以表格表示当x变化时,f'(x),f(x)的变化情况,由表格即可求出单调区间;
(2)借助(1)问的结论,按照函数零点的存在条件,分情况进行讨论,可证明.
点评:本题考查函数的零点存在条件以及利用导数研究函数的单调性问题,本题中渗透了分类讨论思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目