题目内容
已知函数f(x)是偶函数,当x>0时, ,又x∈[-3,-1]时,a≤f(x)≤b恒成立,则b-a的取值范围是________.
,又x∈[-3,-1]时,a≤f(x)≤b恒成立,则b-a的取值范围是________.
[1,+∞)
分析:要使x∈[-3,-1]时,a≤f(x)≤b恒成立,则函数的值域是[a,b]的子集,因此关键是求出函数在x∈[-3,-1]时,函数的值域,利用函数f(x)是偶函数,当x>0时, ,可求.
,可求.
解答:设x<0,则-x>0,
∵x>0时, ,∴
,∴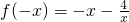
∵函数f(x)是偶函数,∴x<0时,
当x∈[-3,-1]时,函数的值域为[4,5]
∵x∈[-3,-1]时,a≤f(x)≤b恒成立
∴[4,5]⊆[a,b]
∴b-a≥1
故答案为[1,+∞)
点评:本题的考点是函数恒成立问题.主要考查x∈[-3,-1]时,a≤f(x)≤b恒成立,关键是求出函数在x∈[-3,-1]时,函数的值域,利用函数的值域是[a,b]的子集求解.
分析:要使x∈[-3,-1]时,a≤f(x)≤b恒成立,则函数的值域是[a,b]的子集,因此关键是求出函数在x∈[-3,-1]时,函数的值域,利用函数f(x)是偶函数,当x>0时,
 ,可求.
,可求.解答:设x<0,则-x>0,
∵x>0时,
 ,∴
,∴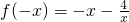
∵函数f(x)是偶函数,∴x<0时,

当x∈[-3,-1]时,函数的值域为[4,5]
∵x∈[-3,-1]时,a≤f(x)≤b恒成立
∴[4,5]⊆[a,b]
∴b-a≥1
故答案为[1,+∞)
点评:本题的考点是函数恒成立问题.主要考查x∈[-3,-1]时,a≤f(x)≤b恒成立,关键是求出函数在x∈[-3,-1]时,函数的值域,利用函数的值域是[a,b]的子集求解.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目