题目内容

已知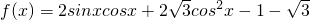 $数学公式$ ，x∈[0， $数学公式$ ]
（1）求f（x）的最大值及此时x的值；
（2）求f（x）在定义域上的单调递增区间．

解：（1）f（x）=sin2x+ $\text{[math]}$ cos2x-1=2sin（2x+ $\text{[math]}$ ）-1，∵0≤x≤ $\text{[math]}$ ，∴ $\text{[math]}$ ≤2x+ $\text{[math]}$ ≤ $\text{[math]}$ ，
当 2x+ $\text{[math]}$ = $\text{[math]}$ 时，即 x= $\text{[math]}$ 时，f（x）有最大值为 1．
（2）由 $\text{[math]}$ ≤2x+ $\text{[math]}$ ≤ $\text{[math]}$ ，得 0≤x≤ $\text{[math]}$ ，
∴f（x）在定义域上的单调递增区间[0， $\text{[math]}$ ]．
分析：（1）利用二倍角公式及两角和的正弦公式化简f（x）为 2sin（2x+ $\text{[math]}$ ）-1，据 $\text{[math]}$ ≤2x+ $\text{[math]}$ ≤ $\text{[math]}$ ，得到
当 2x+ $\text{[math]}$ = $\text{[math]}$ 时，（x）有最大值为 1．
（2）由 $\text{[math]}$ ≤2x+ $\text{[math]}$ ≤ $\text{[math]}$ ，得到 0≤x≤ $\text{[math]}$ ，可得单调递增区间．
点评：本题考查正弦函数的单调性及最值，二倍角公式及两角和的正弦公式，利用单调性求出f（x）的最大值，是解题的难点．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

已知M={x|0≤x≤1}，N={x|x≥p}，若M∩N=∅，则p满足（　　）

已知对于?x∈[0，1]，不等式2^ax²+4x（x-1）+4^-a（x-1）²＞0恒成立，则实数a的取值范围是

（-∞，-2）

（-∞，-2）

已知A={x|0≤x≤4}，B={y|0≤y≤2}，从A到B的对应法则分别是：(1)f：x→y=

x，(2)f：x→y=x-2，(3)f：x→y=

，(4)f：x→y=|x-2|
其中能构成一一映射的是

已知P={x|0≤x≤5}，Q={y|0≤y≤3}，下列不表示从P到Q的函数的是（　　）

（2012•浦东新区二模）已知函数y=f（x），x∈D，如果对于定义域D内的任意实数x，对于给定的非零常数m，总存在非零常数T，恒有f（x+T）＞m•f（x）成立，则称函数f（x）是D上的m级类增周期函数，周期为T．若恒有f（x+T）=m•f（x）成立，则称函数f（x）是D上的m级类周期函数，周期为T．
（1）试判断函数f（x）=log

(x-1)是否为（3，+∞）上的周期为1的2级类增周期函数？并说明理由；
（2）已知函数f（x）=-x²+ax是[3，+∞）上的周期为1的2级类增周期函数，求实数a的取值范围；
（3）下面两个问题可以任选一个问题作答，如果你选做了两个，我们将按照问题（Ⅰ）给你记分．
（Ⅰ）已知T=1，y=f（x）是[0，+∞）上m级类周期函数，且y=f（x）是[0，+∞）上的单调递增函数，当x∈[0，1）时，f（x）=2^x，求实数m的取值范围．
（Ⅱ）已知当x∈[0，4]时，函数f（x）=x²-4x，若f（x）是[0，+∞）上周期为4的m级类周期函数，且y=f（x）的值域为一个闭区间，求实数m的取值范围．